
【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关心的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄 |
|
|
|
|
|
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 |
|
|
|
|
|
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在![]() ,
,![]() 的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(Ⅰ)求年龄在![]() 的被调查者中选取的2人都赞成“延迟退休”的概率;
的被调查者中选取的2人都赞成“延迟退休”的概率;
(Ⅱ)若选中的4人中,不赞成“延迟退休”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
科目:高中数学 来源: 题型:
【题目】【2014陕西理8】原命题为“若![]() 互为共轭复数,则
互为共轭复数,则![]() ”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
A. 真,假,真 B. 假,假,真
C. 真,真,假 D. 假,假,假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)向量a=(x,1),b=(1,y),c=(2,-4),且a⊥c,b∥c,求|a+b|和a+b与c的夹角;
(2)设O为△ABC的外心,已知AB=3,AC=4,非零实数x,y满足![]() =x
=x![]() +y
+y![]() ,且x+2y=1,求cos ∠BAC的值.
,且x+2y=1,求cos ∠BAC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前三项与数列{bn}的前三项相同,且a1+2a2+22a3+…+2n-1an=8n对任意n∈N*都成立,数列{bn+1-bn}是等差数列.
(1)求数列{an}与{bn}的通项公式;
(2)是否存在k∈N*,使得(bk-ak)∈(0,1)?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔场有一边长为20m的正三角形湖面ABC(如图所示),计划筑一条笔直的堤坝DE将水面分成面积相等的两部分,以便进行两类水产品养殖试验(D在AB上,E在AC上).

(1)为了节约开支,堤坝应尽可能短,请问该如何设计?堤坝最短为多少?
(2)将DE设计为景观路线,堤坝应尽可能长,请问又该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
(1)证明:a>0;
(2)若z=a+2b,求z的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网络购物已经成为一种时尚,电商们为了提升知名度,加大了在媒体上的广告投入.经统计,近五年某电商在媒体上的广告投入费用x(亿元)与当年度该电商的销售收入y(亿元)的数据如下表:):
年份 | 2012年 | 2013年 | 2014 | 2015 | 2016 |
广告投入x | 0.8 | 0.9 | 1 | 1.1 | 1.2 |
销售收入y | 16 | 23 | 25 | 26 | 30 |
(1)求y关于x的回归方程; (2)2017年度该电商准备投入广告费1.5亿元,
利用(1)中的回归方程,预测该电商2017年的销售收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: 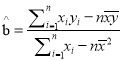
![]() ,选用数据:
,选用数据: ![]() ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com