
【题目】某渔场有一边长为20m的正三角形湖面ABC(如图所示),计划筑一条笔直的堤坝DE将水面分成面积相等的两部分,以便进行两类水产品养殖试验(D在AB上,E在AC上).

(1)为了节约开支,堤坝应尽可能短,请问该如何设计?堤坝最短为多少?
(2)将DE设计为景观路线,堤坝应尽可能长,请问又该如何设计?
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
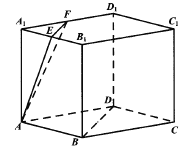
【题目】底面为菱形的直棱柱![]()
中, ![]()
分别为棱![]()
的中点.
(1)在图中作一个平面![]()
,使得![]()
,且平面![]()
.(不必给出证明过程,只要求作出![]()
与直棱柱![]()
的截面).
(2)若![]()
,求平面![]()
与平面![]()
的距离![]()
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两种坐标系中的长度单位相同,已知曲线
轴的正半轴,两种坐标系中的长度单位相同,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)直线 (
(![]() 为参数)与曲线
为参数)与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关心的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄 |
|
|
|
|
|
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 |
|
|
|
|
|
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在![]() ,
,![]() 的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(Ⅰ)求年龄在![]() 的被调查者中选取的2人都赞成“延迟退休”的概率;
的被调查者中选取的2人都赞成“延迟退休”的概率;
(Ⅱ)若选中的4人中,不赞成“延迟退休”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国个人所得税》规定,公民月工资、薪金所得不超过3500元的部分不纳税,超过3500元的部分为全月纳税所得额,此项税款按下表分段累计计算:

已知张先生的月工资、薪金所得为10000元,问他当月应缴纳多少个人所得税?
设王先生的月工资、薪金所得为![]() 元,当月应缴纳个人所得税为
元,当月应缴纳个人所得税为![]() 元,写出
元,写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)已知王先生一月份应缴纳个人所得税为303元,那么他当月的个工资、薪金所得为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①![]() ;②当
;②当![]() 时,
时, ![]() ;③
;③![]() ;④当
;④当![]() 秒时,
秒时, ![]() ∽
∽![]() ;⑤当
;⑤当![]() 的面积为
的面积为![]() 时,时间
时,时间![]() 的值是
的值是![]() 或
或![]() ;其中正确的结论是( )
;其中正确的结论是( )
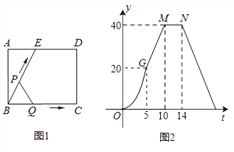
A. ①⑤ B. ②⑤ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高职院校进行自主招生文化素质考试,考试内容为语文、数学、英语三科,总分为200分.现从上线的考生中随机抽取20人,将其成绩用茎叶图记录如下:
男 | 女 | |||||||||||
15 | 6 | |||||||||||
5 | 4 | 16 | 3 | 5 | 8 | |||||||
8 | 2 | 17 | 2 | 3 | 6 | 8 | 8 | 8 | ||||
6 | 5 | 18 | 5 | 7 | ||||||||
19 | 2 | 3 | ||||||||||
(Ⅰ)计算上线考生中抽取的男生成绩的方差![]() ;(结果精确到小数点后一位)
;(结果精确到小数点后一位)
(Ⅱ)从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会,求所选考生恰为一男一女的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
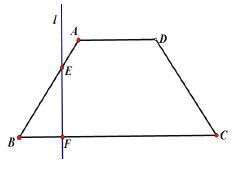
【题目】如图,已知底角为![]() 的等腰梯形
的等腰梯形![]() ,底边
,底边![]() 长为12,腰长为
长为12,腰长为![]() ,当一条垂直于底边
,当一条垂直于底边![]() (垂足为
(垂足为![]() )的直线
)的直线![]() 从左至右移动(与梯形
从左至右移动(与梯形![]() 有公共点)时,直线
有公共点)时,直线![]() 把梯形分成两部分.
把梯形分成两部分.
(1)令![]() ,试写出直线右边部分的面积
,试写出直线右边部分的面积![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)在(1)的条件下,令![]() .构造函数
.构造函数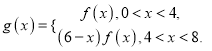
①判断函数![]() 在
在![]() 上的单调性;
上的单调性;
②判断函数![]() 在定义域内是否具有单调性,并说明理由.
在定义域内是否具有单调性,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com