
【题目】已知数列{an}的前三项与数列{bn}的前三项相同,且a1+2a2+22a3+…+2n-1an=8n对任意n∈N*都成立,数列{bn+1-bn}是等差数列.
(1)求数列{an}与{bn}的通项公式;
(2)是否存在k∈N*,使得(bk-ak)∈(0,1)?请说明理由.
【答案】(1)an=24-n(n∈N*), bn=n2-7n+14(n∈N*).(2)不存在k∈N*,使得(bk-ak)∈(0,1)
【解析】
试题分析:(1)利用a1+2a2+22a3+…+2n-1an=8n推出n-1时的表达式,然后作差求出数列{an}的通项公式,利用数列{bn+1-bn}是等差数列利用累加法求出{bn}的通项公式;(2)化简![]() 通过k≥4时,
通过k≥4时,![]() 单调递增,且f(4)=1,所以k≥4时,f(k)≥1,结合f(1)=f(2)=f(3)=0,说明不存在k∈N*,使得(bk-ak)∈(0,1).
单调递增,且f(4)=1,所以k≥4时,f(k)≥1,结合f(1)=f(2)=f(3)=0,说明不存在k∈N*,使得(bk-ak)∈(0,1).
试题解析:(1)已知得a1+2a2+22a3+…+2n-1an
=8n(n∈N*),①
当n≥2时,a1+2a2+22a3+…+2n-2an-1=8(n-1).②
由①-②,得2n-1an=8.∴an=24-n.
在①中,令n=1,得a1=8=24-1,
∴an=24-n(n∈N*).
由题意知b1=8,b2=4,b3=2,
∴b2-b1=-4,b3-b2=-2,
∴数列{bn+1-bn}的公差为-2-(-4)=2.
∴bn+1-bn=-4+(n-1)×2=2n-6.
∴bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)
=8+(-4)+(-2)+…+(2n-8)
=n2-7n+14(n∈N*).
(2)∵bk-ak=k2-7k+14-24-k,
设f(k)=k2-7k+14-24-k,
当k≥4时,f(k)=(k-![]() )2+
)2+![]() -24-k,单调递增,
-24-k,单调递增,
且f(4)=1.
∴k≥4时,f(k)=k2-7k+4-24-k≥1.
又f(1)=f(2)=f(3)=0, ∴不存在k∈N*,使得(bk-ak)∈(0,1).


科目:高中数学 来源: 题型:
【题目】已知随机变量![]() 的取值为不大于
的取值为不大于![]() 的非负整数值,它的分布列为:
的非负整数值,它的分布列为:
| 0 | 1 | 2 |
| n |
|
|
|
|
|
|
其中![]() (
(![]() )满足:
)满足: ![]() ,且
,且![]() .
.
定义由![]() 生成的函数
生成的函数![]() ,令
,令![]() .
.
(I)若由![]() 生成的函数
生成的函数![]() ,求
,求![]() 的值;
的值;
(II)求证:随机变量![]() 的数学期望
的数学期望![]() ,
, ![]() 的方差
的方差![]() ;
;
(![]() )
)
(Ⅲ)现投掷一枚骰子两次,随机变量![]() 表示两次掷出的点数之和,此时由
表示两次掷出的点数之和,此时由![]() 生成的函数记为
生成的函数记为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有4个人参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择,为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(1) 求出4个人中恰有2个人去 参加甲游戏的概率;
(2)求这4个人中去参加甲游戏人数大于去参加乙游戏的人数的概率;
(3)用![]() 分别表示这4个人中去参加甲、乙游戏的人数,记
分别表示这4个人中去参加甲、乙游戏的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关心的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄 |
|
|
|
|
|
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 |
|
|
|
|
|
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在![]() ,
,![]() 的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(Ⅰ)求年龄在![]() 的被调查者中选取的2人都赞成“延迟退休”的概率;
的被调查者中选取的2人都赞成“延迟退休”的概率;
(Ⅱ)若选中的4人中,不赞成“延迟退休”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
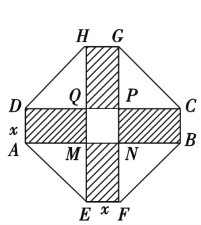
【题目】某居民小区要建造一座八边形的休闲小区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的,是面积为200平方米的十字形地带.计划在正方MNPQ上建一座花坛,造价是每平方米4 200元,在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价是每平方米210元,再在四个空角上铺上草坪,造价是每平方米80元.
(1)设总造价是S元,AD长为x米,试建立S关于x的函数关系式;
(2)当x为何值时,S最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() ,设函数
,设函数![]() .
.
(1)若函数![]() 的图象关于直线
的图象关于直线![]() 对称,且
对称,且![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)在(1)的条件下,当![]() 时,函数
时,函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com