
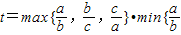 ,
,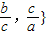 .
.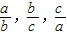 }和min{
}和min{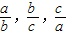 }的值,即可算出总有实数t=1成立,得到本题答案;
}的值,即可算出总有实数t=1成立,得到本题答案; }=c且min{
}=c且min{ }=
}= ,因此对c<b2和c≥b2两种情况加以讨论,利用三角形两边之和大于第三边和不等式的性质进行推导,联解不等式组可得t的取值范围是[1,
,因此对c<b2和c≥b2两种情况加以讨论,利用三角形两边之和大于第三边和不等式的性质进行推导,联解不等式组可得t的取值范围是[1,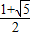 ).
).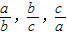 }=min{
}=min{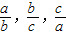 }=1
}=1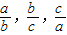 }•min{
}•min{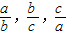 }=1;
}=1; }=
}=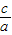 ,min{
,min{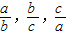 }=
}=
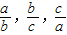 }•min{
}•min{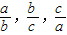 }=
}=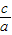 •
•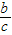 =
= =1;
=1;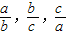 }=
}= ,min{
,min{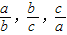 }=
}=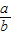
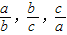 }•min{
}•min{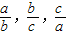 }=
}= •
•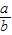 =
= =1
=1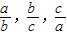 }=max{
}=max{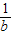 ,
,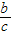 ,c}=c
,c}=c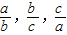 }=min{
}=min{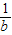 ,
, ,c}=
,c}=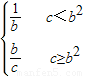
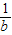 =
=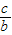 ,可得c=tb,(t≥1)
,可得c=tb,(t≥1)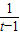
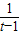 ,解之得1<t<
,解之得1<t<
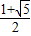 )
)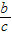 =b,可得
=b,可得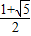
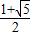 ,得此时t的范围为[1,
,得此时t的范围为[1,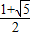 )
)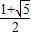 ).
). )
)

科目:高中数学 来源: 题型:
| a |
| b |
| b |
| c |
| c |
| a |
| a |
| b |
| b |
| c |
| c |
| a |
| A、充分布不必要的条件 |
| B、必要而不充分的条件 |
| C、充要条件 |
| D、既不充分也不必要的条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| b |
| c |
| c |
| a |
| a |
| b |
| b |
| c |
| c |
| a |
1+
| ||
| 2 |
1+
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| b |
| c |
| c |
| a |
| a |
| b |
| b |
| c |
| c |
| a |
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学选修2-1 1.2充分条件与必要条件练习卷(解析版) 题型:选择题
记实数x1,x2,…,xn中的最大数为max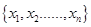 ,最小数为
,最小数为
min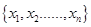 .已知△ABC的三边边长为a,b,c(a≤b≤c),定义它的倾斜度为
.已知△ABC的三边边长为a,b,c(a≤b≤c),定义它的倾斜度为
l=max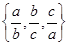 ·min
·min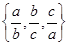 ,
,
则“l=1”是“△ABC为等边三角形”的( )
A.必要而不充分条件
B.充分而不必要条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com