
设a=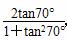 ,b=
,b=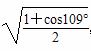 ,c=
,c=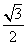 cos81°+
cos81°+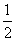 sin99°,将a、b、c用“<”号连接起来________.
sin99°,将a、b、c用“<”号连接起来________.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
2010年7月1日某人到银行存入一年期款a元,若年利率为x,按复利计算,则到2015年7月1日可取款( )
A.a(1+x)5元 B.a(1+x)6元
C.a+(1+x)5元 D.a(1+x5)元
查看答案和解析>>
科目:高中数学 来源: 题型:
已知α为锐角,且2tan(π-α)-3cos( +β)+5=0,tan(π+α)+6sin(π+β)=1,则sinα的值是( )
+β)+5=0,tan(π+α)+6sin(π+β)=1,则sinα的值是( )
A.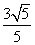 B.
B.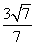
C. D.
D.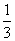
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,a、b、c分别是角A、B、C的对边,向量m=(b,2a-c),n=(cosB,cosC),且m∥n.
(1)求角B的大小;
(2)设f(x)=cos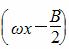 +sinωx(ω>0),且f(x)的最小正周期为π,求f(x)在区间[0,
+sinωx(ω>0),且f(x)的最小正周期为π,求f(x)在区间[0, ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com