练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．某夏令营由三个中学的学生构成，其中一中学生（编号001--123），二中学生（编号124--246），三中学生（编号247--360），现用系统抽样方法从中抽取60人进行调查问卷．已知002号学生被抽中，则二中共被抽中（　　）人．
    A．18B．19C．20D．21

    分析 根据题意得出构成以2为首项，6为公差的等差数列，通项为6n-4，即可得出结论．

    解答 解：依题意可知，在随机抽样中，首次抽到002号，以后每隔6个号抽到一个人，
    则构成以2为首项，6为公差的等差数列，通项为6n-4，
    由124≤6n-4≤246，可得22≤n≤41，
    ∴二中共被抽中41-22+1=20人．
    故选C．

    点评 本题考查系统抽样方法，考查学生的计算能力，确定构成以2为首项，6为公差的等差数列，通项为6n-4是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．已知O是锐角△ABC的外接圆圆心，$tanA=\frac{{\sqrt{2}}}{2}$，若$\frac{cosB}{sinC}\overrightarrow{AB}+\frac{cosC}{sinB}\overrightarrow{AC}=2m\overrightarrow{AO}$，则m的值为（　　）
    A．1B．$\frac{{\sqrt{3}}}{3}$C．$\frac{{\sqrt{3}}}{6}$D．$\frac{{\sqrt{3}}}{12}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．f（x）是定义在R上的奇函数，且f（x-3）=f（x+3），当0＜x＜3时，f（x）=2-log2（x+2），则当0＜x＜6时，不等式（x-3）f（x）＞0的解集是（　　）
    A．（0，2）∪（3，4）B．（0，2）∪（4，5）C．（2，3）∪（4，5）D．（2，3）∪（3，4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．某校在一次期末数学测试中，为统计学生的考试情况，从学校的2000
    名学生中随机抽取50名学生的考试成绩，被测学生成绩全部介于60分到140分之间（满分150分），将统计结果按如下方式分成八组：第一组，如图是按上述分组方法得到的频率分布直方图的一部分．
    （1）求第七组的频率，并完成频率分布直方图；
    （2）估计该校的2000名学生这次考试成绩的平均分（可用中值代替各组数据平均值）；
    （3）若从样本成绩属于第一组和第六组的所有学生中随机抽取2名，求他们的分差小于10分的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

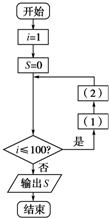    18．如图是求从1到100中所有自然数的平方和而设计的程序框图，将空白处补充完整，并指明它是循环结构中的哪一种类型，且画出它的另一种结构框图．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知某乡农田有山地8000亩，丘陵12000亩，平地24000亩，洼地4000亩．现抽取农田480亩估计全乡农田粮食平均亩产量，则采用（　　）抽样比较合适．
    A．抽签法B．随机数表法C．系统抽样法D．分层抽样法

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知函数f（x）=$\left\{\begin{array}{l}{x+4，（x≤-1）}\\{{x}^{2}，（-1＜x＜1）}\\{2x，（x≥1）}\end{array}\right.$，若f（m）=$\frac{1}{2}$，则m所有可能值的和为（　　）
    A．-$\frac{7}{2}$B．2C．-$\frac{13}{4}$D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

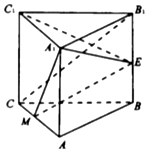    12．如图，在三棱柱ABC-A1B1C1中，已知侧棱与底面垂直，∠CAB=90°，且AC=1，AB=2，E为BB1的中点，M为AC上的一点，$\overrightarrow{AM}$=$\frac{2}{3}$$\overrightarrow{AC}$．
    （Ⅰ）证明：CB1∥平面A1EM；
    （Ⅱ）若A1A的长度为$\sqrt{2}$，求三棱锥E-C1A1M的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=|x-2|+|x+1|．
    （1）求不等式f（x）＞7的解集；
    （2）若实数m，n＞0，且f（x）的最小值为m+n，求m2+n2的最小值，并指出此时m，n的值．

    查看答案和解析>>

    同步练习册答案