Question

1．在平面直角坐标系xoy中，点${F_1}（{-\sqrt{3}，0}）$，圆F₂：x²+y²-2$\sqrt{3}$x-13=0，以动点P为圆心的圆经过点F₁，且圆P与圆F₂内切．
（1）求动点的轨迹的方程；
（2）若直线l过点（1，0），且与曲线E交于A，B两点，则在x轴上是否存在一点D（t，0）（t≠0），使得x轴平分∠ADB？若存在，求出t的值；若不存在，请说明理由．

Answer 1

分析 （1）化圆的方程为标准方程，求出圆心坐标和半径，画出图形，数形结合可得|PF₁|+|PF₂|=4＞|F₁F₂|，故点P的轨迹是以F₁、F₂为焦点，长轴长为4的椭圆，
由此求出动点的轨迹方程；
（2）设A（x₁，y₁），B（x₂，y₂），当直线l的斜率不为0时，设直线l：x=ny+1．联立直线方程与椭圆方程，化为关于y的一元二次方程，利用根与系数的关系求得A，B的纵坐标的和与积，结合斜率关系求得t值；当直线l的斜率为0时，直线为x轴，取A（-2，0），B（2，0），满足∠ODA=∠ODB．综上，在x轴上存在一点D（4，0），使得x轴平分∠ADB．

解答 解：（1）圆F₂：x²+y²-2$\sqrt{3}$x-13=0化为$（x-\sqrt{3}）^{2}+{y}^{2}=16$．
故F₂（$\sqrt{3}，0$），半径r=4．
而$|{F}_{1}{F}_{2}|=2\sqrt{3}$＜4，∴点F₁在圆F₂内，
又由已知得圆P的半径R=|PF₁|，由圆P与圆F₂内切得，圆P内切于圆F₂，即|PF₂|=4-|PF₁|，
∴|PF₁|+|PF₂|=4＞|F₁F₂|，
故点P的轨迹是以F₁、F₂为焦点，长轴长为4的椭圆，
有c=$\sqrt{3}$，a=2，则b²=a²-c²=1．
故动点的轨迹方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$；
（2）设A（x₁，y₁），B（x₂，y₂），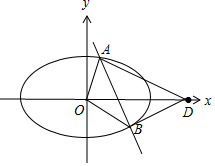
当直线l的斜率不为0时，设直线l：x=ny+1．
联立$\left\{\begin{array}{l}{x=ny+1}\\{{x}^{2}+4{y}^{2}-4=0}\end{array}\right.$，得（n²+4）y²+2ny-3=0．
△=16（n²+3）＞0恒成立．
${y}_{1}+{y}_{2}=\frac{-2n}{{n}^{2}+4}$，${y}_{1}{y}_{2}=\frac{-3}{{n}^{2}+4}$．①
设直线DA、DB的斜率分别为k₁，k₂，则由∠ODA=∠ODB得，
${k}_{1}+{k}_{2}=\frac{{y}_{1}}{{x}_{1}-t}+\frac{{y}_{2}}{{x}_{2}-t}$=$\frac{{y}_{1}（{x}_{2}-t）+{y}_{2}（{x}_{1}-t）}{（{x}_{1}-t）（{x}_{2}-t）}$
=$\frac{{y}_{1}（n{y}_{2}+1-t）+{y}_{2}（n{y}_{1}+1-t）}{（{x}_{1}-t）（{x}_{2}-t）}$=$\frac{2n{y}_{1}{y}_{2}+（1-t）（{y}_{1}+{y}_{2}）}{（{x}_{1}-t）（{x}_{2}-t）}=0$．
∴2ny₁y₂+（1-t）（y₁+y₂）=0，②
联立①②，得n（t-4）=0．
故存在t=4满足题意；
当直线l的斜率为0时，直线为x轴，取A（-2，0），B（2，0），满足∠ODA=∠ODB．
综上，在x轴上存在一点D（4，0），使得x轴平分∠ADB．

点评 本题考查椭圆轨迹方程的求法，考查直线与椭圆位置关系的应用，考查数形结合的解题思想方法，是中档题．