
| A. | 3+$\frac{\sqrt{3}}{2}$ | B. | 2+$\sqrt{3}$ | C. | 2+$\frac{\sqrt{6}}{2}$ | D. | 3+$\sqrt{3}$ |
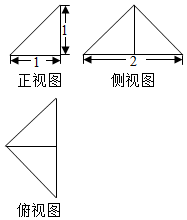
分析 由三视图知该几何体是一个三棱锥,由三视图求出几何元素的长度、并判断出线面位置关系,由勾股定理和三角形的面积公式求出各个面的面积,并加起来求出几何体的表面积.
解答 解: 根据三视图可知几何体是一个三棱锥,直观图如图所示:
根据三视图可知几何体是一个三棱锥,直观图如图所示:
且D是AB的中点,PD⊥平面ABC,PD=AD=BD=CD=1,
∴PD⊥CD,PD⊥AB,由勾股定理得,PA=PB=PC=$\sqrt{2}$,
由俯视图得,CD⊥AB,则AC=BC=$\sqrt{2}$,
∴几何体的表面积S=$2×\frac{1}{2}×2×1$+$2×\frac{1}{2}×\sqrt{2}×\sqrt{2}×\frac{\sqrt{3}}{2}$
=2+$\sqrt{3}$,
故选:B.
点评 本题考查三视图求几何体的表面积,由三视图正确复原几何体是解题的关键,考查空间想象能力.


科目:高中数学 来源: 题型:解答题
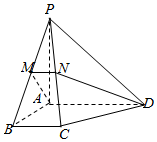 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
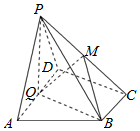 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢运动 | 不喜欢运动 | 总计 | |
| 男 | a= | b= | |
| 女 | c= | d= | |
| 总计 | n= |
| P(χ2≥x0) | 0.050 | 0.025 | 0.010 | 0.001 |
| x0 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 男生 | 15 | 35 | 50 |
| 女生 | 30 | 40 | 70 |
| 总计 | 45 | 75 | 120 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在地平线上 | B. | 仰角为30° | C. | 仰角为45° | D. | 仰角为60° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A真包含于B | B. | A=B | C. | A⊆B | D. | 无法比较 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com