
 如图所示,椭圆E的中心为坐标原点,焦点F1,F2在x轴上,且F1在抛物线y2=4x的准线上,点P是椭圆E上的一个动点,△PF1F2面积的最大值为$\sqrt{3}$.
如图所示,椭圆E的中心为坐标原点,焦点F1,F2在x轴上,且F1在抛物线y2=4x的准线上,点P是椭圆E上的一个动点,△PF1F2面积的最大值为$\sqrt{3}$.分析 (1)设椭圆E的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),求得抛物线的准线方程,可得c=1,当P是椭圆短轴顶点时,△PF1F2面积取得最大,可得b,由a,b,c的关系可得a,进而得到椭圆方程;
(2)①四边形ABCD不是菱形.由(1)可得F1(-1,0),AB不平行于x轴,可设AB:x=my-1,代入椭圆方程,运用韦达定理,连接OA,OB,若四边形ABCD是菱形,则OA⊥OB,即$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,即有x1x2+y1y2=0,化简整理,代入韦达定理,解方程即可判断;
②易知四边形ABCD为平行四边形,则四边形ABCD面积S=4S△AOB,运用三角形的面积公式可得S=2|OF1|•|y1-y2|=2$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$,代入韦达定理,令t=1+m2(t≥1),可得t的函数式,运用导数判断单调性,即可得到所求最大值.
解答 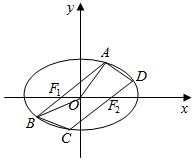 解:(1)设椭圆E的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
解:(1)设椭圆E的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
F1在抛物线y2=4x的准线x=-1上,可得c=1,
当P是椭圆短轴顶点时,△PF1F2面积取得最大,
且为$\frac{1}{2}$•2c•b=$\sqrt{3}$,可得b=$\sqrt{3}$,
则a=$\sqrt{{b}^{2}+{c}^{2}}$=2,即有椭圆E的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)①四边形ABCD不是菱形.
理由:由(1)可得F1(-1,0),AB不平行于x轴,可设AB:x=my-1,
代入椭圆方程,可得(4+3m2)y2-6my-9=0,
设A(x1,y1),B(x2,y2),即有y1+y2=$\frac{6m}{4+3{m}^{2}}$,y1y2=-$\frac{9}{4+3{m}^{2}}$,
连接OA,OB,若四边形ABCD是菱形,则OA⊥OB,
即$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,即有x1x2+y1y2=0,
由x1x2=(my1-1)(my2-1)=m2y1y2+1-m(y1+y2)=$\frac{4-12{m}^{2}}{4+3{m}^{2}}$,
即有$\frac{-5-12{m}^{2}}{4+3{m}^{2}}$=0,显然无实数解,
故四边形ABCD不是菱形;
②易知四边形ABCD为平行四边形,则四边形ABCD面积S=4S△AOB,
|OF1|=1,S=2|OF1|•|y1-y2|=2$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$
=2$\sqrt{\frac{36{m}^{2}}{(4+3{m}^{2})^{2}}+\frac{36}{4+3{m}^{2}}}$=24$\sqrt{\frac{1+{m}^{2}}{(4+3{m}^{2})^{2}}}$,
令t=1+m2(t≥1),即有S=24$\sqrt{\frac{t}{(3t+1)^{2}}}$=24$\sqrt{\frac{1}{9t+\frac{1}{t}+6}}$,
由f(t)=9t+$\frac{1}{t}$,f′(t)=9-$\frac{1}{{t}^{2}}$>0在t≥1成立,即有f(t)在[1,+∞)递增,
可得t=1,即m=0时,四边形ABCD的面积取得最大值6.
点评 本题考查椭圆的方程的求法,注意运用抛物线的准线方程和椭圆的性质,考查四边形的面积的最值的求法,注意运用直线方程和椭圆方程联立,运用韦达定理和弦长公式,考查导数的运用及函数的单调性,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
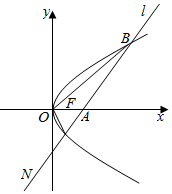 如图,已知抛物线C以坐标原点O为顶点,焦点F在x轴的正半轴上,且|OF|=$\frac{1}{2}$.
如图,已知抛物线C以坐标原点O为顶点,焦点F在x轴的正半轴上,且|OF|=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
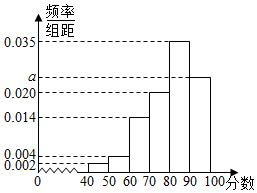 2015年,威海智慧公交建设项目已经基本完成.为了解市民对该项目的满意度,分别从不同公交站点随机抽取若干市民对该项目进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
2015年,威海智慧公交建设项目已经基本完成.为了解市民对该项目的满意度,分别从不同公交站点随机抽取若干市民对该项目进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:| 满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 11日 | 12日 | 13日 | 14日 | 15日 |
| 平均气温x(℃) | 9 | 10 | 12 | 11 | 8 |
| 销量y(杯) | 23 | 25 | 30 | 26 | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
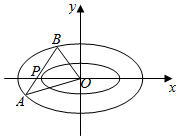 设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1的离心率e=$\frac{1}{2}$,动点P在椭圆C上,点P到椭圆C的两个焦点的距离之和是4.
设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1的离心率e=$\frac{1}{2}$,动点P在椭圆C上,点P到椭圆C的两个焦点的距离之和是4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com