
分析 (I)设等差数列{an}的公差为d,由a4+a7=20,对任意的k∈N都有Sk+1=3Sk+k2.可得2a1+9d=20,S2=3S1+1即d=a1+1,联立解出即可得出.
(II)由an≥m,可得:2n-1≥m,可得:n≥$\frac{m+1}{2}$.当m=2k-1时,k∈N*,2mbm=k,可得bm=$\frac{m+1}{{2}^{m+1}}$.当m=2k时,k∈N*,2mbm=k+1,可得bm=$\frac{m+2}{{2}^{m+1}}$.即可得出bm.当k∈N*时,(-1)2k-1-1b2k-1+(-1)2k-1b2k=$\frac{k-1}{{2}^{2k}}$.利用分组求和、“错位相减法”、等比数列的前n项和公式即可得出.
解答 解:(I)设等差数列{an}的公差为d,∵a4+a7=20,对任意的k∈N都有Sk+1=3Sk+k2.
∴2a1+9d=20,S2=3S1+1即a1+a2=3a1+1,亦即d=a1+1,联立解得a1=1,d=2,
∴an=1+2(n-1)=2n-1.
(II)由an≥m,可得:2n-1≥m,解得:n≥$\frac{m+1}{2}$.
当m=2k-1时,k∈N*,2mbm=k,即bm=$\frac{k}{{2}^{m}}$=$\frac{m+1}{{2}^{m+1}}$.
当m=2k时,k∈N*,2mbm=k+1,即bm=$\frac{k+1}{{2}^{m}}$=$\frac{\frac{m}{2}+1}{{2}^{m}}$=$\frac{m+2}{{2}^{m+1}}$.
∴bm=$\left\{\begin{array}{l}{\frac{m+1}{{2}^{m+1}},m为奇数}\\{\frac{m+2}{{2}^{m+1}},m为偶数}\end{array}\right.$.
当k∈N*时,(-1)2k-1-1b2k-1+(-1)2k-1b2k=$\frac{2k}{{2}^{2k}}$-$\frac{2k+2}{{2}^{2k+1}}$=$\frac{k-1}{{2}^{2k}}$.
∴T2m=(b1-b2)+(b3-b4)+…+(b2m-1-b2m)=$\frac{0}{{2}^{2}}$+$\frac{1}{{2}^{4}}$+$\frac{2}{{2}^{6}}$+…+$\frac{m-2}{{2}^{2m-2}}$+$\frac{m-1}{{2}^{2m}}$,
即T2m=0+$\frac{1}{{2}^{4}}$+$\frac{2}{{2}^{6}}$+…+$\frac{m-2}{{2}^{2m-2}}$+$\frac{m-1}{{2}^{2m}}$,
$\frac{1}{{2}^{2}}$T2m=0+$\frac{1}{{2}^{6}}$+$\frac{2}{{2}^{8}}$+…+$\frac{m-2}{{2}^{2m}}$+$\frac{m-1}{{2}^{2m+2}}$,
∴$\frac{3}{4}$T2m=$\frac{1}{{2}^{4}}$+$\frac{1}{{2}^{6}}$+…+$\frac{1}{{2}^{2m}}$-$\frac{m-1}{{2}^{2m+2}}$=$\frac{\frac{1}{{2}^{4}}(1-\frac{1}{{2}^{2m-2}})}{1-\frac{1}{4}}$-$\frac{m-1}{{2}^{2m+2}}$=$\frac{1}{12}$-$\frac{3m+1}{3×{2}^{2m+2}}$,
∴T2m=$\frac{1}{9}$$(1-\frac{3m+1}{{4}^{m}})$.
点评 本题考查了分组求和、“错位相减法”、等差数列与等比数列的提出公式及其前n项和公式,考查了分类讨论方法、推理能力与计算能力,属于难题.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥A-BCD中,BC⊥BD,AD⊥AC,CD=2,∠ACD=30°,∠DCB=45°,AO⊥平面BCD,垂足O恰好在BD上.
如图,在三棱锥A-BCD中,BC⊥BD,AD⊥AC,CD=2,∠ACD=30°,∠DCB=45°,AO⊥平面BCD,垂足O恰好在BD上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 天数x | 3 | 4 | 5 | 6 | 7 |
| 繁殖数(千个) | 2.5 | 3 | t | 4.5 | 6 |
| A. | 3.5 | B. | 3.75 | C. | 4 | D. | 4.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,椭圆E的中心为坐标原点,焦点F1,F2在x轴上,且F1在抛物线y2=4x的准线上,点P是椭圆E上的一个动点,△PF1F2面积的最大值为$\sqrt{3}$.
如图所示,椭圆E的中心为坐标原点,焦点F1,F2在x轴上,且F1在抛物线y2=4x的准线上,点P是椭圆E上的一个动点,△PF1F2面积的最大值为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
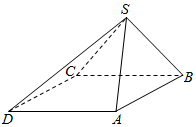 四棱锥S-ABCD中,底面ABCD为平行四边形,已知∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC.
四棱锥S-ABCD中,底面ABCD为平行四边形,已知∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com