
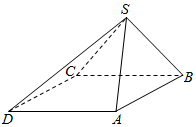
 四棱锥S-ABCD中,底面ABCD为平行四边形,已知∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC.
四棱锥S-ABCD中,底面ABCD为平行四边形,已知∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC.分析 (1)由已知可得AB∥CD,从而可证AB∥平面SCD,利用线面平行的性质即可证明l∥AB.
(2)连接AC,由已知利用余弦定理得AC=2,可证AC=AB,取BC中点G,连接SG,AG,则AG⊥BC,通过证明BC⊥平面SAG,即可证明BC⊥SA.
解答 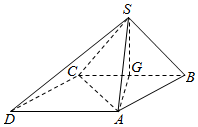 (本题满分为12分)
(本题满分为12分)
解:(1)证明:∵底面ABCD为平行四边形,
∴AB∥CD,
∵AB?平面SCD,CD?平面SCD,
∴AB∥平面SCD,
又∵平面SCD与平面SAB的交线为l,
∴l∥AB.…(6分)
(2)证明:连接AC,∵∠ABC=45°,AB=2,BC=2$\sqrt{2}$,
由余弦定理得AC=2,
∴AC=AB,
取BC中点G,连接SG,AG,则AG⊥BC,
∵SG∩AG=G,
∴BC⊥平面SAG,
∴BC⊥SA…(12分)
点评 本题主要考查了线面平行的性质,线面垂直的性质,考查了空间想象能力和推理论证能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 11日 | 12日 | 13日 | 14日 | 15日 |
| 平均气温x(℃) | 9 | 10 | 12 | 11 | 8 |
| 销量y(杯) | 23 | 25 | 30 | 26 | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1的离心率e=$\frac{1}{2}$,动点P在椭圆C上,点P到椭圆C的两个焦点的距离之和是4.
设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1的离心率e=$\frac{1}{2}$,动点P在椭圆C上,点P到椭圆C的两个焦点的距离之和是4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{5}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | S≤$\frac{3}{4}$? | B. | S≤$\frac{11}{12}$? | C. | S≤$\frac{25}{24}$? | D. | S≤$\frac{137}{120}$? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com