
分析 (I)由条件求得A的值,利用正弦定理求得B的值.
(II)利用三角恒等变换化简函数的解析式,再利用正弦函数的定义域和值域,求得f(x)在区间$[{\frac{π}{2},\frac{17π}{24}}]$上的取值范围.
解答 解:(I)∵$f(A-\frac{π}{4})=2\sqrt{2}sin({A-\frac{π}{4}})cosA=0$,∴$sin({A-\frac{π}{4}})=0或cosA=0$,∴$在三角形中,得A=\frac{π}{4}或\frac{π}{2}$.
∵△ABC中,BC=2,AB=$\sqrt{2}$,∴当A=$\frac{π}{2}$时,△ABC为等腰直角三角形,B=$\frac{π}{4}$;
当A=$\frac{π}{4}$时,由正弦定理可得$\frac{2}{sin\frac{π}{4}}$=$\frac{\sqrt{2}}{sinC}$,
求得sinC=$\frac{1}{2}$,∴C=$\frac{π}{6}$ 或C=$\frac{5π}{6}$(舍去),∴B=π-A-C=$\frac{7π}{12}$.
综上可得,B=$\frac{π}{4}$ 或B=$\frac{7π}{12}$.
(II)$f(x)=2\sqrt{2}sinx({\frac{{\sqrt{2}}}{2}cosx-\frac{{\sqrt{2}}}{2}sinx})=2sinxcosx-2{sin^2}x$=$sin2x+cos2x-1=\sqrt{2}({\frac{{\sqrt{2}}}{2}sin2x+\frac{{\sqrt{2}}}{2}cos2x})-1=\sqrt{2}sin({2x+\frac{π}{4}})-1$,
∵$\frac{π}{2}≤x≤\frac{17π}{24}$,∴$\frac{5π}{4}≤2x+\frac{π}{4}≤\frac{5π}{3}$,∴$-\sqrt{2}≤\sqrt{2}sin({2x+\frac{π}{4}})≤-1$,∴-$\sqrt{2}$-1≤sin(2x-$\frac{π}{4}$)≤-2.
由正弦函数的性质可知,$当2x+\frac{π}{4}=\frac{3π}{2},即x=\frac{5π}{8}时,f(x)取最小值-\sqrt{2}-1$;$当2x+\frac{π}{4}=\frac{5π}{4},即x=\frac{π}{2}时,f(x)取最大值-2$.
所以,f(x)在区间$[{\frac{π}{2},\frac{17π}{24}}]$上的取值范围是$[{-\sqrt{2}-1,-2}]$.
点评 本题主要考查正弦定理、三角恒等变换,正弦函数的定义域和值域,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,在三棱锥A-BCD中,BC⊥BD,AD⊥AC,CD=2,∠ACD=30°,∠DCB=45°,AO⊥平面BCD,垂足O恰好在BD上.
如图,在三棱锥A-BCD中,BC⊥BD,AD⊥AC,CD=2,∠ACD=30°,∠DCB=45°,AO⊥平面BCD,垂足O恰好在BD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
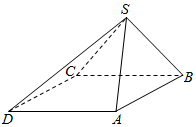 四棱锥S-ABCD中,底面ABCD为平行四边形,已知∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC.
四棱锥S-ABCD中,底面ABCD为平行四边形,已知∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com