
分析 (1)由已知求得a,把已知的坐标代入椭圆方程得到关于a,b的关系式,把a代入求得b,则椭圆方程可求;
(2)求出N的坐标,设出NE所在直线方程,与椭圆方程联立求得E的坐标,同理求得F的坐标,代入两点求斜率公式可得直线EF的斜率为定值.
解答 解:(1)依据椭圆的定义2a=4⇒a=2,
∵$M({\frac{1}{2},\frac{{3\sqrt{5}}}{4}})$在椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$上,
∴$\frac{1}{4{a}^{2}}+\frac{45}{16{b}^{2}}=1$,把a=2代入可得b2=3.
∴椭圆方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)由(1)得,c=1,则N(1,$\frac{3}{2}$),
设直线NE的方程为:$y=k(x-1)+\frac{3}{2}$,
代入$\frac{x^2}{4}+\frac{y^2}{3}=1$,得$(3+4{k^2}){x^2}+4k(3-2k)x+4{({\frac{3}{2}-k})^2}-12=0$.
设E(xE,yE),F(xF,yF),
∵点$N({1,\frac{3}{2}})$在椭圆上,
∴由韦达定理得:${x_E}+1=-\frac{4k(3-2k)}{{3+4{k^2}}}$.
∴${x_E}=\frac{{4{{({\frac{3}{2}-k})}^2}-12}}{{3+4{k^2}}},{y_E}=k{x_E}+\frac{3}{2}-k$.
又直线NF的斜率与NE的斜率互为相反数,
在上式中以-k代k,可得${x_F}=\frac{{4{{({\frac{3}{2}+k})}^2}-12}}{{3+4{k^2}}},{y_F}=-k{x_F}+\frac{3}{2}+k$,
∴xF+xE=$\frac{8{k}^{2}-6}{3+4{k}^{2}}$,${x}_{F}-{x}_{E}=\frac{24k}{3+4{k}^{2}}$..
∴直线EF的斜率${k}_{EF}=\frac{{y}_{F}-{y}_{E}}{{x}_{F}-{x}_{E}}=\frac{-k({x}_{F}+{x}_{E})}{{x}_{F}-{x}_{E}}$$+\frac{2k}{{x}_{F}-{x}_{E}}$
=$\frac{-k•\frac{8{k}^{2}-6}{3+4{k}^{2}}+2k}{\frac{24k}{3+4{k}^{2}}}=\frac{1}{2}$,
即直线EF的斜率为定值,其值为$\frac{1}{2}$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,考查计算能力,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}-1$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,椭圆E的中心为坐标原点,焦点F1,F2在x轴上,且F1在抛物线y2=4x的准线上,点P是椭圆E上的一个动点,△PF1F2面积的最大值为$\sqrt{3}$.
如图所示,椭圆E的中心为坐标原点,焦点F1,F2在x轴上,且F1在抛物线y2=4x的准线上,点P是椭圆E上的一个动点,△PF1F2面积的最大值为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
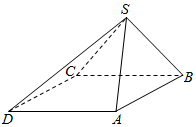 四棱锥S-ABCD中,底面ABCD为平行四边形,已知∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC.
四棱锥S-ABCD中,底面ABCD为平行四边形,已知∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0} | B. | {0,1} | C. | {-1,0,1} | D. | {-1,0,1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com