
分析 通过作差、变形可知(an$+\frac{1}{{a}^{n}}$)-(a+$\frac{1}{a}$)=(an-a)•$\frac{{a}^{n+1}-1}{{a}^{n+1}}$,分0<a<1、a>1两种情况讨论,定号即得结论.
解答 证明:(an$+\frac{1}{{a}^{n}}$)-(a+$\frac{1}{a}$)=(an-a)+($\frac{1}{{a}^{n}}$-$\frac{1}{a}$)
=(an-a)+$\frac{a-{a}^{n}}{{a}^{n+1}}$
=(an-a)(1-$\frac{1}{{a}^{n+1}}$)
=(an-a)•$\frac{{a}^{n+1}-1}{{a}^{n+1}}$,
∵a>0且a≠1,
∴0<a<1或a>1,
当0<a<1时,an-a<0、an+1-1<0,
∴an$+\frac{1}{{a}^{n}}$>a+$\frac{1}{a}$(n>2,n∈N);
当a>1时,an-a>0、an+1-1>0,
∴an$+\frac{1}{{a}^{n}}$>a+$\frac{1}{a}$(n>2,n∈N);
综上所述,an$+\frac{1}{{a}^{n}}$>a+$\frac{1}{a}$(n>2,n∈N).
点评 本题考查用比较法证明不等式,作差、变形、定号是一般步骤,注意解题方法的积累,属于中档题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
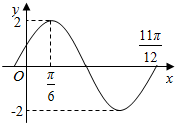 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,若方程f(x)=m在区间[0,π]上有两个不同的数解x1、x2,则x1+x2的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,若方程f(x)=m在区间[0,π]上有两个不同的数解x1、x2,则x1+x2的值为( )| A. | $\frac{π}{3}$ | B. | $\frac{2}{3}π$ | C. | $\frac{4}{3}π$ | D. | $\frac{π}{3}$或$\frac{4}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com