
分析 画出曲线y= $\sqrt{1-{x}^{2}}$的图象,数形结合分析k的取值范围,进而表示出△AOB的面积,利用基本不等式可得答案.
解答 解:曲线y= $\sqrt{1-{x}^{2}}$的图象如图所示:
若直线l与曲线相交于A,B两点,
则直线l的斜率k<0,
设l:y=k(x- $\sqrt{2}$),则点O到l的距离d=$\frac{\sqrt{2}k}{\sqrt{1+{k}^{2}}}$,
则△AOB的面积S=$\frac{1}{2}$•|AB|•d=$\frac{1}{2}$•2$\sqrt{(1-{d}^{2})}$•d=$\sqrt{(1-{d}^{2}){d}^{2}}$≤$\frac{1-{d}^{2}+{d}^{2}}{2}$=$\frac{1}{2}$,
当且仅当1-d2=d2,即d=$\frac{\sqrt{2}k}{\sqrt{1+{k}^{2}}}$=$\frac{\sqrt{2}}{2}$时,S最最大值,
解得:k=-$\frac{\sqrt{3}}{3}$.
点评 本题考查的知识点是点到直线的距离公式,直线与圆的位置关系,基本不等式,难度中档.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
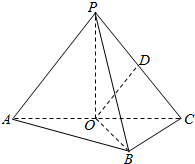 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
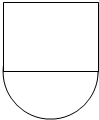 以长为2的铁丝围成上部为矩形,下部为半圆形的框架,如果半圆的直径为2x,求此框架围成图形(如图所示)的面积为y与x的函数关系式y=f(x),并写出它的定义域.
以长为2的铁丝围成上部为矩形,下部为半圆形的框架,如果半圆的直径为2x,求此框架围成图形(如图所示)的面积为y与x的函数关系式y=f(x),并写出它的定义域.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com