
分析 (1)化根式为分数指数幂,然后利用有理指数幂的运算性质求得答案;
(2)对a分类,然后利用指数式的单调性化指数不等式为一次不等式求解.
解答 解:(1)$\root{3}{{a}^{\frac{9}{2}}\sqrt{{a}^{-3}}}$÷$\sqrt{\root{3}{{a}^{-7}}•\root{3}{{a}^{13}}}$
=$({a}^{\frac{9}{2}}•{a}^{-\frac{3}{2}})^{\frac{1}{3}}$$÷({a}^{-\frac{7}{3}}•{a}^{\frac{13}{3}})^{\frac{1}{2}}$
=1;
(2)当a>1时,原不等式可变为x+5<4x-1,解得x>2;
当0<a<1时,原不等式可变为x+5>4x-1,解得x<2.
故当a>1时,原不等式的解集为(2,+∞);
当0<a<1时,原不等式的解集为(-∞,2).
点评 本题考查有理指数幂的化简与求值,考查了指数不等式的解法,是基础题.


科目:高中数学 来源:2016-2017学年湖南益阳市高二9月月考数学(理)试卷(解析版) 题型:选择题
函数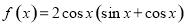 的最大值和最小正周期分别是 ( )
的最大值和最小正周期分别是 ( )
A.2,π B.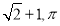 C. 2,2π D.
C. 2,2π D.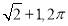
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
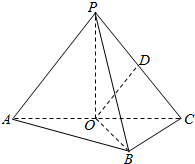 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{9}$,+∞) | B. | (-∞,$\frac{1}{9}$] | C. | [$\frac{10}{9}$,+∞) | D. | (-∞,$\frac{10}{9}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com