
分析 (1)由题意可得|$\frac{27}{5}$-2|<a,且|6-2|≥a,由此求得a的范围,再结合a∈N*,可得a的值.
(2)由条件利用绝对值的意义|x+4|+|x-2|的最小值,可得m的范围.
解答 解:(1)由题意可得|$\frac{27}{5}$-2|<a,且|6-2|≥a,求得$\frac{17}{5}$<a≤4.
再结合a∈N*,可得a=4.
(2)由题意可得关于x的不等式|x+4|+|x-2|<m有解,而|x+4|+|x-2|表示数轴上的x对应点到-4、2对应点的距离之和,它的最小值为6,
故m>6.
点评 本题主要考查绝对值不等式的解法,绝对值的意义,函数的恒成立问题,属于中档题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
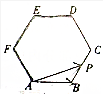 如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=k,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$,0]∪[k,$\frac{3}{2}{k}^{2}$].
如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=k,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$,0]∪[k,$\frac{3}{2}{k}^{2}$].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{5}$i | B. | $\frac{3}{5}$i | C. | i | D. | -i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com