
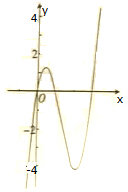
 已知函数f(x)=2x(x-1)(x-3)的图象如图所示,有以下关于方程f(x)+1=0的说法:①有2个实数根;②当x>0时,有1个实数根;③当-1<x<0时,有1个实数根;④当x>1时,有1个实数根;⑤当-1<x<3时,有3个实数根.其中正确说法的序号是③⑤(填上所有正确命题的序号).
已知函数f(x)=2x(x-1)(x-3)的图象如图所示,有以下关于方程f(x)+1=0的说法:①有2个实数根;②当x>0时,有1个实数根;③当-1<x<0时,有1个实数根;④当x>1时,有1个实数根;⑤当-1<x<3时,有3个实数根.其中正确说法的序号是③⑤(填上所有正确命题的序号). 分析 求出导数,求得单调区间和极值,方程f(x)+1=0的根即为函数y=f(x)和直线y=-1的交点的横坐标.作出直线y=-1,可得三个交点,其横坐标设为a,b,c,且-1<a<0,1<b<2,2<c<3.对选项一一加以判断,即可得到结论.
解答 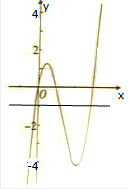 解:函数f(x)=2x(x-1)(x-3)的导数为f′(x)=2(3x2-8x+3),
解:函数f(x)=2x(x-1)(x-3)的导数为f′(x)=2(3x2-8x+3),
当f′(x)=0时,x=$\frac{4±\sqrt{7}}{3}$,
由f(x)在($\frac{4-\sqrt{7}}{3}$,$\frac{4+\sqrt{7}}{3}$)递减,在(-∞,$\frac{4-\sqrt{7}}{3}$),($\frac{4+\sqrt{7}}{3}$,+∞)递增,
即有x=$\frac{4-\sqrt{7}}{3}$取得极大值,x=$\frac{4+\sqrt{7}}{3}$取得极小值,如图.
方程f(x)+1=0的根即为函数y=f(x)和直线y=-1的交点的横坐标.
作出直线y=-1,可得三个交点,其横坐标设为a,b,c,
且-1<a<0,1<b<2,2<c<3.
则①不正确,有3个实数根;②不正确,x>0时,有两个实数根;
③-1<x<0,有1个实数根,正确;④x>1,有两个实数根,不正确;
⑤当-1<x<3时,有3个实数根,正确.
故答案为:③⑤
点评 本题考查函数方程的转化思想的运用,考查方程的根的个数的判断,注意运用数形结合的思想方法,属于基础题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com