
分析 (1)利用向量垂直与数量积的关系、向量三角形法则即可得出.
(2)利用三角形面积计算公式、余弦定理即可得出.
解答 (1)证明:∵$\overrightarrow{OA}$$⊥\overrightarrow{BC}$,$\overrightarrow{OB}$⊥$\overrightarrow{AC}$,
∴$\overrightarrow{OA}$•$\overrightarrow{BC}$=0,$\overrightarrow{OB}$•$\overrightarrow{AC}$=0,
∴0=$\overrightarrow{OA}$•$\overrightarrow{BC}$=$(\overrightarrow{OC}+\overrightarrow{CA})$$•\overrightarrow{BC}$=$\overrightarrow{OC}•\overrightarrow{BC}$+$\overrightarrow{CA}•\overrightarrow{BC}$,
0=$\overrightarrow{OB}$•$\overrightarrow{AC}$=$(\overrightarrow{OC}+\overrightarrow{CB})$•$\overrightarrow{AC}$=$\overrightarrow{OC}•\overrightarrow{AC}$+$\overrightarrow{CB}•\overrightarrow{AC}$,
∴$\overrightarrow{OC}$$\overrightarrow{BC}$-$\overrightarrow{OC}•\overrightarrow{AC}$=0,∴$\overrightarrow{OC}•\overrightarrow{BA}$=0,∴$\overrightarrow{OC}$⊥$\overrightarrow{AB}$.
(2)设△ABC面积为S,由面积公式可知$\left\{\begin{array}{l}{\frac{1}{2}×\frac{1}{13}×AB=S}\\{\frac{1}{2}×\frac{1}{11}×AC=S}\\{\frac{1}{2}×\frac{1}{5}×BC=S}\end{array}\right.$,
∴AB=26S,AC=22S,BC=10S,
∴∠C为最大角,
∴cosC=$\frac{(22S)^{2}+(10S)^{2}-(26S)^{2}}{2×22S×10S}$=-$\frac{23}{110}$.
点评 本题考查了向量垂直与数量积的关系、向量三角形法则、三角形面积计算公式、余弦定理,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
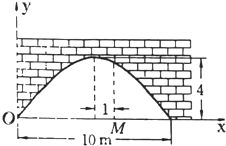 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 4m,跨度为 10m,把它的图形放在如图所示直角坐标系中.
有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 4m,跨度为 10m,把它的图形放在如图所示直角坐标系中.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}和1$ | B. | $\sqrt{3}和\frac{3}{2}$ | C. | $\sqrt{2}和\frac{3}{2}$ | D. | 2和1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com