
分析 (Ⅰ)曲线C2的方程为ρsin2θ=2pcosθ(p>0),即为ρ2sin2θ=2pρcosθ(p>0),利用互化公式可得直角坐标方程.将曲线C1的参数方程$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}t}\\{y=-4+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数)与抛物线方程联立得:${t}^{2}-12\sqrt{2}$t+32=0,可得|PA|+|PB|=|t1|+|t2|=|t1+t2|.
(Ⅱ)将曲线C1的参数方程与y2=2px联立得:t2-2$\sqrt{2}$(4+p)t+32=0,又|PA|,|AB|,|PB|成等比数列,可得|AB|2=|PA||PB|,可得$|{t}_{1}-{t}_{2}{|}^{2}$=|t1||t2|,即$({t}_{1}+{t}_{2})^{2}$=5t1t2,利用根与系数的关系即可得出.
解答 解:(Ⅰ)∵曲线C2的方程为ρsin2θ=2pcosθ(p>0),即为ρ2sin2θ=2pρcosθ(p>0),
∴曲线C2的直角坐标方程为y2=2px,p>2.
又已知p=2,∴曲线C2的直角坐标方程为y2=4x.
将曲线C1的参数方程$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}t}\\{y=-4+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数)与y2=4x联立得:${t}^{2}-12\sqrt{2}$t+32=0,
由于△=$(-12\sqrt{2})^{2}$-4×32>0,
设方程两根为t1,t2,
∴t1+t2=12$\sqrt{2}$,t1•t2=32,
∴|PA|+|PB|=|t1|+|t2|=|t1+t2|=12$\sqrt{2}$.
(Ⅱ)将曲线C1的参数方程$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}t}\\{y=-4+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数)与y2=2px联立得:t2-2$\sqrt{2}$(4+p)t+32=0,
由于△=$[-2\sqrt{2}(4+p)]^{2}$-4×32=8(p2+8p)>0,
∴t1+t2=2$\sqrt{2}$(4+p),t1•t2=32,
又|PA|,|AB|,|PB|成等比数列,
∴|AB|2=|PA||PB,
∴$|{t}_{1}-{t}_{2}{|}^{2}$=|t1||t2|,
∴$({t}_{1}+{t}_{2})^{2}$=5t1t2,
∴$[-2\sqrt{2}(4+p)]^{2}$=5×32,
∴p2+8p-4=0,解得:p=-4$±2\sqrt{5}$,
又p>0,
∴p=-4+2$\sqrt{5}$,
∴当|PA|,|AB|,|PB|成等比数列时,p的值为-4+2$\sqrt{5}$.
点评 本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、参数方程的应用、弦长公式、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cardA=5 | B. | cardB=3 | C. | card(A∩B)=2 | D. | card(A∪B)=5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
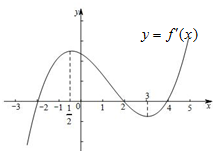 如果函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列判断:
如果函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列判断:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com