
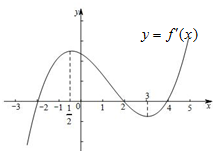
 如果函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列判断:
如果函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列判断:分析 直接由导函数的图象分析①②⑤;再由导函数的符号得到原函数的单调区间,从而判断③④的正误.
解答 解:由函数y=f′(x)的图象可得,
y=f′(x)在区间(-3,-$\frac{1}{2}$)内单调递增,故①正确;
函数y=f′(x)在区间(-$\frac{1}{2}$,3)内单调递减,故②正确;
由上可知,当x=-$\frac{1}{2}$时,函数y=f′(x)有极大值,故⑤正确;
当x∈(-∞,-2)∪(2,4)时,f′(x)<0,
当x∈(-2,2)∪(4,+∞)时,f′(x)>0,
∴函数y=f(x)在区间(4,5)内单调递增,故③正确;
函数y=f(x)在区间(-2,2)内单调递增,在(2,4)内单调递减,当x=2时,函数y=f(x)有极大值,故④错误;
∴正确的判断是①②③⑤.
故答案为:①②③⑤.
点评 本题考查利用导数研究函数的单调性,考查了学生读取图表的能力,是基础题.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | $\frac{3}{4}$ | C. | $\sqrt{5}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
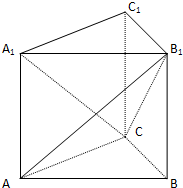 直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,$A{B_1}=\sqrt{3}$.
直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,$A{B_1}=\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com