
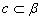
解法一:(反证法)
假设MN与PQ共面于β,则点M、N、P、Q∈β.
又点N、Q∈b![]()
![]()
![]()
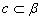 ,同理
,同理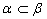 ,∴a、b、C共面,与已知a、b、C不共面矛盾,故MN与PQ为异面直线.
,∴a、b、C共面,与已知a、b、C不共面矛盾,故MN与PQ为异面直线.
解法二:
![]() 点Q
点Q![]() MN.
MN.
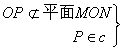
![]() 点P
点P![]() 平面MON.
平面MON.
故平面MON内一点Q与平面外一点P的连线PQ,与平面内不过Q点的直线MN是异面直线.
点评:(1)证明两条直线异面通常用反证法,反证法是一种间接证法,在立体几何证题中经常用到,在运用反证法时,一定要严格按照步骤分层次进行.
(2)利用反证法证明两条直线异面,有两种假设:一是假设两直线共面;二是假设两直线平行或相交,必须指出,后一种假设往往不如前一种假设优越.
(3)定理法也是判断两直线异面的一种重要方法,运用时,要积极寻找定理的条件.


科目:高中数学 来源: 题型:
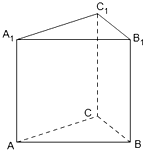 如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.
如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.查看答案和解析>>
科目:高中数学 来源:2008-2009学年宁夏银川市六盘山中学高一(下)第二次月考数学试卷(必修2)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com