
【题目】已知函数f(x)=x2+(1﹣a)x+(1﹣a).a∈R.
(1)当a=4时,解不等式f(x)≥7;
(2)若对P任意的x∈(﹣1,+∞),函数f(x)的图象恒在x轴上方,求实数a的取值范围.
【答案】
(1)解:当a=4是,f(x)=x2﹣3x﹣3≥7x2﹣3x﹣10≥0
∴x≥5或 x≤﹣2.
故不等式解集为{x|x≥5或 x≤﹣2}
(2)解:∵x∈(﹣1,+∞)时,函数f(x)的图象恒在x轴上方,
∴f(x)=x2+(1﹣a)x+(1﹣a)≥0
x2+x+1≥a(x+1)
∵x>﹣1∴x+1>0
∴a≤ ![]()
∵ ![]() ≥
≥ ![]()
当且仅当x+1= ![]() ,即x=0时取等号.
,即x=0时取等号.
∴a≤1
【解析】(1)当a=4时,转化为x2﹣3x﹣10≥0解不等式;(2)函数f(x)的图象恒在x轴上方转化为f(x)≥0(x>﹣1)恒成立,x2+x+1≥a(x+1)
在(﹣1,+∞)恒成立,再分离参数∴a≤ ![]() ,求解.
,求解.
【考点精析】认真审题,首先需要了解二次函数的性质(当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减).
上递减).


科目:高中数学 来源: 题型:
【题目】某地区上年度电价为0.8元/kWh,年用电量为akWh,本年度计划将电价降到0.55 元/kWh至0.75元/kWh之间,而用户期待电价为0.4元/kWh,下调电价后新增加的用电量与实际电价和用户期望电价的差成反比(比例系数为K),该地区的电力成本为0.3元/kWh.(注:收益=实际用电量×(实际电价﹣成本价)),示例:若实际电价为0.6元/kWh,则下调电价后新增加的用电量为 ![]() 元/kWh)
元/kWh)
(1)写出本年度电价下调后,电力部门的收益y与实际电价x的函数关系;
(2)设K=0.2a,当电价最低为多少仍可保证电力部门的收益比上一年至少增长20%?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|,g(x)=x2+2ax+1(a为正常数),且函数f(x)和g(x)的图象与y轴的交点重合.
(1)求a实数的值
(2)若h(x)=f(x)+b ![]() (b为常数)试讨论函数h(x)的奇偶性;
(b为常数)试讨论函数h(x)的奇偶性;
(3)若关于x的不等式f(x)﹣2 ![]() >a有解,求实数a的取值范围.
>a有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点O,焦点在![]() 轴上,离心率为
轴上,离心率为![]() 的椭圆C过点
的椭圆C过点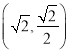
(Ⅰ)求椭圆C的方程;
(Ⅱ)设不过坐标原点O的直线与椭圆C交于P,Q两点,若![]() ,证明:点O到直线
,证明:点O到直线![]() 的距离为定值.
的距离为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆曲线方程为 ![]() ,两焦点分别为F1 , F2 .
,两焦点分别为F1 , F2 .
(1)若n=﹣1,过左焦点为F1且斜率为 ![]() 的直线交圆锥曲线于点A,B,求△ABF2的周长.
的直线交圆锥曲线于点A,B,求△ABF2的周长.
(2)若n=4,P圆锥曲线上一点,求PF1PF2的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,a≠1且loga3>loga2,若函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为1.
(1)求a的值;
(2)解不等式 ![]() ;
;
(3)求函数g(x)=|logax﹣1|的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosC+(cosA﹣ ![]() sinA)cosB=0.
sinA)cosB=0.
(1)求角B的大小;
(2)若b= ![]() ,c=1,求△ABC的面积.
,c=1,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com