


 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
 为了了解某校今年高三男生的身体状况,随机抽查了部分男生,将测得的他们的体重(单位:千克)数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了了解某校今年高三男生的身体状况,随机抽查了部分男生,将测得的他们的体重(单位:千克)数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:
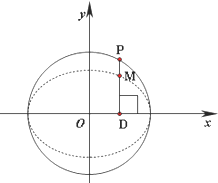 如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且
如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且| DM |
| ||
| 2 |
| DP |
| OA |
| OB |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
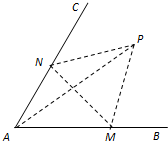 如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).查看答案和解析>>
科目:高中数学 来源: 题型:
| PC |
| BC |
| PB |
| CB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com