
如图,在四棱锥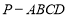 中,底面
中,底面 是菱形,
是菱形, ,且侧面
,且侧面 平面
平面 ,点
,点 是棱
是棱 的中点.
的中点.

(1)求证: 平面
平面 ;
;
(2)求证: ;
;
(3)若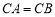 ,求证:平面
,求证:平面 平面
平面 .
.
(1)证明见解析;(2)证明见解析;(3)证明见解析
【解析】
试题分析:(1)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;(2)证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形的底边上的高,中线和顶角的角平分线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形等等;(3)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化;(4)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键.
试题解析:【解析】
(1)因为底面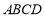 是菱形,
是菱形,
所以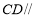
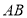 .
.
又因为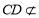 平面
平面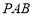 ,
,
所以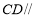 平面
平面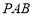 .
.

(2)因为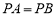 ,点
,点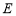 是棱
是棱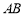 的中点,
的中点,
所以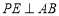 .
.
因为平面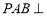 平面
平面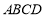 ,平面
,平面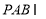 平面
平面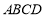
 ,
,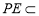 平面
平面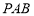 ,
,
所以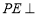 平面
平面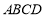 ,
,
因为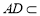 平面
平面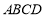 ,
,
所以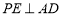 .
.
(3)因为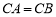 ,点
,点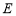 是棱
是棱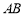 的中点,
的中点,
所以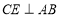 .
.
由(2)可得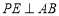 ,
,
所以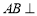 平面
平面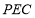 ,
,
又因为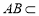 平面
平面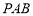 ,
,
所以平面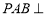 平面
平面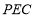 .
.
考点:1、直线与平面平行的判定;2、直线与直线垂直的判定;3、平面与平面垂直的判定.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源:2015届福建省、德化一中高三9月摸底考试理科数学试卷(解析版) 题型:选择题
已知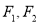 分别是双曲线
分别是双曲线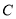 :
: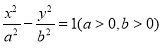 的左右焦点,以
的左右焦点,以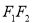 为直径的圆与双曲线
为直径的圆与双曲线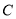 在第二象限的交点为
在第二象限的交点为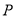 ,若双曲线的离心率为5,则
,若双曲线的离心率为5,则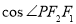 等于
等于
A.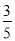 B.
B.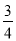 C.
C.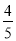 D.
D.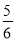
查看答案和解析>>
科目:高中数学 来源:2015届福建省、德化一中高三9月摸底考试理科数学试卷(解析版) 题型:选择题
“ ”是“
”是“ ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届福建省八县(市高三上学期半期联考理科数学试卷(解析版) 题型:选择题
若存在对于定义域为 的函数
的函数 ,若存在非零实数
,若存在非零实数 ,使函数
,使函数 在
在 和
和
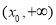 上均有零点,则称
上均有零点,则称 为函数
为函数 的一个“纽点”.则下列四个函数中,不存在“纽
的一个“纽点”.则下列四个函数中,不存在“纽
点”的是( )
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高三第一次诊断考试理科数学试卷(解析版) 题型:解答题
已知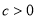 ,设命题
,设命题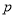 :函数
:函数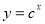 为减函数.命题
为减函数.命题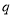 :当
:当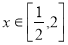 时,函数
时,函数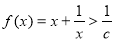 恒成立.如果“p或q”为真命题,“p且q”为假命题,求c的取值范围.
恒成立.如果“p或q”为真命题,“p且q”为假命题,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com