
分析 (1)设等差数列{an}的公差为d,运用等差数列的通项公式,计算即可得到;
(2)由等差数列的求和公式和数列的单调性,可得Tn的最大值,再由恒成立思想,即可得到m的范围.
解答 解:(1)设等差数列{an}的公差为d,
由a2=6,a3+a6=27.可得a1+d=6,2a1+7d=27,
解得a1=d=3,
即有an=a1+(n-1)d=3n;
(2)Tn=$\frac{{S}_{n}}{3•{2}^{n-1}}$=$\frac{\frac{1}{2}(3+3n)n}{3•{2}^{n-1}}$=$\frac{n(n+1)}{{2}^{n}}$,
Tn+1=$\frac{(n+1)(n+2)}{{2}^{n+1}}$,
由$\frac{{T}_{n+1}}{{T}_{n}}$=$\frac{n+2}{2n}$,
可得T1<T2≤T3>T4>T5>…>Tn>…
即有T2=T3=$\frac{3}{2}$,取得最大值.
对于一切正整数n,总有Tn≤m成立,
则有m≥$\frac{3}{2}$.
即有m的取值范围是[$\frac{3}{2}$,+∞).
点评 本题考查等差数列的通项公式和求和公式的运用,考查不等式恒成立问题的解法,注意运用数列的单调性,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
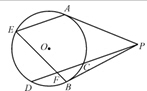 过圆O外一点P向圆引两条切线PA、PB和割线PCD,从A点作弦AE平行于CD,连接BE交CD于F.
过圆O外一点P向圆引两条切线PA、PB和割线PCD,从A点作弦AE平行于CD,连接BE交CD于F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com