
【题目】心理学家分析发现“喜欢空间想象”与“性别”有关,某数学兴趣小组为了验证此结论,从全体组员中按分层抽样的方法抽取50名同学(男生30人、女生20人),给每位同学立体几何题、代数题各一道,让各位同学自由选择一道题进行解答,选题情况统计如下表:(单位:人)
立体几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关?
(2)经统计得,选择做立体几何题的学生正答率为![]() ,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为![]() ,答对文科题的概率均为
,答对文科题的概率均为![]() ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆C: ![]() 的离心率为
的离心率为![]() ,右焦点为(
,右焦点为(![]() ,0).(1)求椭圆C的方程;(2)若过原点
,0).(1)求椭圆C的方程;(2)若过原点![]() 作两条互相垂直的射线,与椭圆交于A,B两点,求证:点O到直线AB的距离为定值.
作两条互相垂直的射线,与椭圆交于A,B两点,求证:点O到直线AB的距离为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
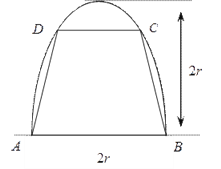
【题目】如图,有一块半椭圆形钢板,其长半轴为![]() ,短半轴为
,短半轴为![]() ,计划将此钢板切割成等腰梯形的形状,下底
,计划将此钢板切割成等腰梯形的形状,下底![]() 是半椭圆的短轴,上底
是半椭圆的短轴,上底![]() 的端点在椭圆上,记
的端点在椭圆上,记![]() ,梯形面积为
,梯形面积为![]() .
.
(Ⅰ)求面积![]() 关于变量
关于变量![]() 的函数表达式,并写出定义域;
的函数表达式,并写出定义域;
(Ⅱ)求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三一次月考之后,为了为解数学学科的学习情况,现从中随机抽出若干名学生此次的数学成绩,按成绩分组,制成了下面频率分布表:
组号 | 分组 | 频数 | 频率 |
第一组 |
| 5 | 0.05 |
第二组 |
| 35 | 0.35 |
第三组 |
| 30 | 0.30 |
第四组 |
| 20 | 0.20 |
第五组 |
| 10 | 0.10 |
合计 | 100 | 1.00 | |
(1)试估计该校高三学生本次月考的平均分;
(2)如果把表中的频率近似地看作每个学生在这次考试中取得相应成绩的概率,那么从所有学生中采用逐个抽取的方法任意抽取3名学生的成绩,并记成绩落在![]() 中的学生数为
中的学生数为![]() ,
,
求:①在三次抽取过程中至少有两次连续抽中成绩在![]() 中的概率;
中的概率;
②![]() 的分布列和数学期望.(注:本小题结果用分数表示)
的分布列和数学期望.(注:本小题结果用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用长为18 m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届江苏如东高级中学等四校高三12月联考】已知数列![]() 满足
满足![]() ,
,![]() ,且对任意
,且对任意![]() ,
,![]() 都有
都有![]() .
.
(1)求![]() ,
,![]() ;
;
(2)设![]() (
(![]() ).
).
①求数列![]() 的通项公式;
的通项公式;
②设数列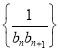 的前
的前![]() 项和
项和![]() ,是否存在正整数
,是否存在正整数![]() ,
,![]() ,且
,且![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等比数列?若存在,求出
成等比数列?若存在,求出![]() ,
,![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com