
【题目】数列![]() 的前
的前![]() 项和记为
项和记为![]() ,
, ![]() ,点
,点![]() 在直线
在直线![]() 上,
上, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,
, ![]() ,
, ![]() 是数列
是数列![]() 的前
的前![]() 项和,求
项和,求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由![]() 在直线
在直线![]() 上可得,
上可得, ![]() ,所以
,所以![]() ,两式相减得
,两式相减得![]() 为等比数列,从而得出
为等比数列,从而得出![]() 的通项公式;(2)求出
的通项公式;(2)求出![]() ,利用分组求和法以及等差数列的求和公式与等比数列的求和公式可得出
,利用分组求和法以及等差数列的求和公式与等比数列的求和公式可得出![]() .
.
试题解析:(1)由题知![]() ,所以
,所以![]() ,两式相减得
,两式相减得
![]() ,又
,又![]() ,
,
所以![]() 是以1为首项,4为公比的等比数列.
是以1为首项,4为公比的等比数列.
![]()
(2)![]() ,
, ![]() ,
,
所以![]()
![]() .
.
【方法点晴】本题主要考查等比数列的定义与通项、等差数列的求和公式与等比数列的求和公式以及利用“分组求和法”求数列前![]() 项和,属于中档题. 利用“分组求和法”求数列前
项和,属于中档题. 利用“分组求和法”求数列前![]() 项和常见类型有两种:一是通项为两个公比不相等的等比数列的和或差,可以分别用等比数列求和后再相加减;二是通项为一个等差数列和一个等比数列的和或差,可以分别用等差数列求和、等比数列求和后再相加减.
项和常见类型有两种:一是通项为两个公比不相等的等比数列的和或差,可以分别用等比数列求和后再相加减;二是通项为一个等差数列和一个等比数列的和或差,可以分别用等差数列求和、等比数列求和后再相加减.


科目:高中数学 来源: 题型:
【题目】在每年的3月份,濮阳市政府都会发动市民参与到植树绿化活动中去林业管理部门为了保证树苗的质量都会在植树前对树苗进行检测,现从甲、乙两种树苗中各抽测了![]() 株树苗,量出它们的高度如下(单位:厘米),
株树苗,量出它们的高度如下(单位:厘米),
甲:37,21,31,20,29,19,32,23,25,33;
乙:10,30,47,27,46,14,26,10,44,46.
(1)画出两组数据的茎叶图并根据茎叶图对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的![]() 株甲种树苗高度平均值为
株甲种树苗高度平均值为![]() ,将这
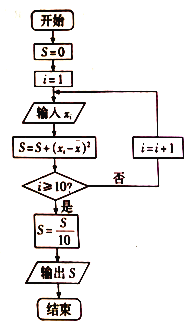
,将这![]() 株树苗的高度依次输人,按程序框(如图)进行运算,问输出的
株树苗的高度依次输人,按程序框(如图)进行运算,问输出的![]() 大小为多少?并说明
大小为多少?并说明![]() 的统计学意义,
的统计学意义,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px过点P(1,1).过点(0, ![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
(Ⅰ)求抛物线C的方程,并求其焦点坐标和准线方程;
(Ⅱ)求证:A为线段BM的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆x2+y2-2y-1=0关于直线y=x对称的圆的方程是 ( )
A. (x-1)2+y2=2 B. (x+1)2+y2=2 C. (x-1)2+y2=4 D. (x+1)2+y2=4
【答案】A
【解析】圆![]() 的标准方程为
的标准方程为![]() ,所以圆心为(0,1),半径为
,所以圆心为(0,1),半径为![]() ,圆心关于直线
,圆心关于直线![]() 的对称点是(1,0),所以圆x2+y2-2y-1=0关于直线y=x对称的圆的方程是
的对称点是(1,0),所以圆x2+y2-2y-1=0关于直线y=x对称的圆的方程是![]() ,选A.
,选A.
点睛:本题主要考查圆关于直线的对称的圆的方程,属于基础题。解答本题的关键是求出圆心关于直线的对称点,两圆半径相同。
【题型】单选题
【结束】
8
【题目】已知双曲线的离心率为![]() ,焦点是
,焦点是![]() ,
, ![]() ,则双曲线方程为 ( )
,则双曲线方程为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马, 田忌的下等马劣于齐王的下等马.现从双方的马匹中随机选一匹进行一场比赛,则田忌的马获胜的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,由直三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中, ![]() ,平面
,平面![]() 平面
平面![]() .
.
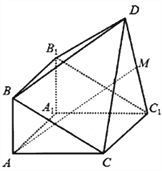
(Ⅰ)求证: ![]() ;
;
(Ⅱ)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com