Question

18．已知边长为a的菱形ABCD中，∠ABC=60°，将该菱形沿对角线AC折起，使BD=a，则三棱锥D-ABC的体积为（　　）

• A． $\frac{a^3}{6}$
• B． $\frac{a^3}{12}$
• C． $\frac{{\sqrt{3}}}{12}{a^3}$
• D． $\frac{\sqrt{2}}{12}{a}^{3}$

Answer 1

分析 由题意可得：三棱锥B-ACD是一个正四面体．如图所示，进而算出高BO，即可计算出体积．

解答 解：由题意可得：三棱锥B-ACD是一个棱长为a的正四面体．如图所示：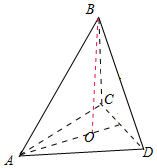
过B点作BO⊥底面ACD，则点O是底面的中心，可知AO=$\frac{2}{3}×\frac{\sqrt{3}}{2}a=\frac{\sqrt{3}}{3}a$．
在Rt△ABO中，由勾股定理得BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=$\sqrt{{a}^{2}-（\frac{\sqrt{3}}{3}a）^{2}}$=$\frac{\sqrt{6}}{3}a$．
∴V=$\frac{1}{3}×\frac{1}{2}×a×a×sin60°×\frac{\sqrt{6}}{3}a$=$\frac{\sqrt{2}}{12}{a}^{3}$．
故选：D．

点评 本题考查三棱锥的体积的求法，考查三棱锥、折叠等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、函数与方程思想、数形结合思想，是中档题．