
【题目】已知函数![]() ,
,![]() ,其导函数为
,其导函数为![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 有两个零点
有两个零点![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)求导得到![]() ,讨论
,讨论![]() 和
和![]() 两种情况,得到答案.
两种情况,得到答案.
(2)![]() ,设
,设![]() ,求导得到单调性得到
,求导得到单调性得到![]() ,得到答案.
,得到答案.
(3)要证![]() ,即
,即![]() ,构造函数
,构造函数![]() ,证明函数单调递减,得到
,证明函数单调递减,得到![]() ,根据单调性得到答案.
,根据单调性得到答案.
(1)![]() ,
,![]() ,
,
当![]() 时,
时,![]() 恒成立,函数单调递增;
恒成立,函数单调递增;
当![]() 时,
时,![]() ,
,![]() ,故
,故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
综上所述:![]() 时,函数在R上单调递增,
时,函数在R上单调递增,![]() 时,函数在
时,函数在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)![]() ,即
,即![]() ,设
,设![]() ,
,
则![]()
设![]() ,则
,则![]() 在
在![]() 上恒成立,故
上恒成立,故![]() 单调递增,
单调递增,
故![]() ,故
,故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
故![]() ,故
,故![]() .
.
(3)![]() ,故
,故![]() ,
,![]() ,相加得到
,相加得到![]() .
.
要证![]() ,即证
,即证![]() ,即
,即![]() .
.
![]() ,即
,即![]() ,设
,设![]() ,则
,则![]() ,
,
函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
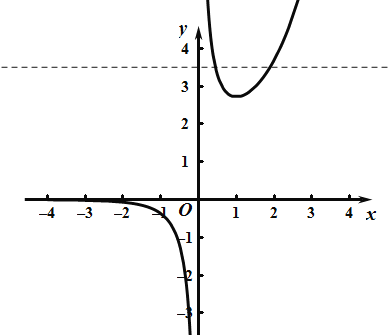
函数图像如图所示:故取![]() ,
,
构造函数![]() ,
,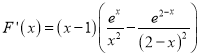 ,
,
![]() ,
,![]() ,函数在
,函数在![]() 上单调递减,故
上单调递减,故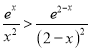 ,
,
当![]() 时,
时,![]() ,函数单调递减,
,函数单调递减,![]() ,故
,故![]() .
.
即![]() ,即
,即![]() ,
,![]() ,
,![]() ,函数单调递增,
,函数单调递增,
故![]() ,即
,即![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图,将使用手机时间不低于80分钟的学生称为“手机迷”.
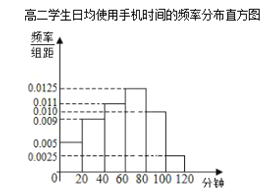
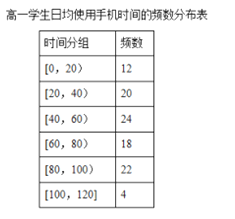
(I)将频率视为概率,估计哪个年级的学生是“手机迷”的概率大?请说明理由.
(II)在高二的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
非手机迷 | 手机迷 | 合计 | |
男 | |||
女 | |||
合计 |
附:随机变量![]() (其中
(其中![]() 为样本总量).
为样本总量).
参考数据 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| span>2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若函数![]() 在区间
在区间![]() (
(![]() 为自然对数的底数)上有唯一的零点,求实数
为自然对数的底数)上有唯一的零点,求实数![]() 的取值范围;
的取值范围;
(2)若在![]() (
(![]() 为自然对数的底数)上存在一点
为自然对数的底数)上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自新型冠状病毒疫情爆发以来,人们时刻关注疫情,特别是治愈率,治愈率![]() 累计治愈人数/累计确诊人数,治愈率的高低是“战役”的重要数据,由于确诊和治愈人数在不断变化,那么人们就非常关心第
累计治愈人数/累计确诊人数,治愈率的高低是“战役”的重要数据,由于确诊和治愈人数在不断变化,那么人们就非常关心第![]() 天的治愈率,以此与之前的治愈率比较,来推断在这次“战役”中是否有了更加有效的手段,下面是一段计算治愈率的程序框图,请同学们选出正确的选项,分别填入①②两处,完成程序框图.( )
天的治愈率,以此与之前的治愈率比较,来推断在这次“战役”中是否有了更加有效的手段,下面是一段计算治愈率的程序框图,请同学们选出正确的选项,分别填入①②两处,完成程序框图.( )
![]() :第
:第![]() 天新增确诊人数;
天新增确诊人数;![]() :第
:第![]() 天新增治愈人数;
天新增治愈人数;![]() :第
:第![]() 天治愈率
天治愈率
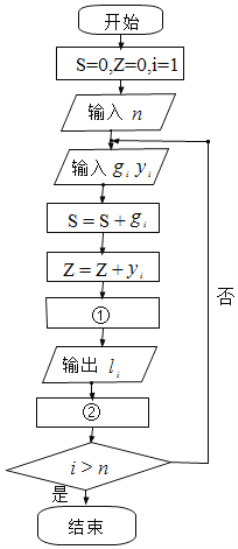
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 是棱
是棱![]() 的中点.
的中点.
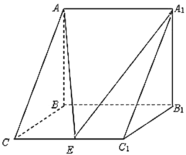
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小姜同学有两个盒子![]() 和
和![]() ,最初盒子
,最初盒子![]() 有6枚硬币,盒子
有6枚硬币,盒子![]() 是空的.在每一回合中,她可以将一枚硬币从
是空的.在每一回合中,她可以将一枚硬币从![]() 盒移到
盒移到![]() 盒,或者从
盒,或者从![]() 盒移走
盒移走![]() 枚硬币,其中
枚硬币,其中![]() 是
是![]() 盒中当前的硬币数.当
盒中当前的硬币数.当![]() 盒空时她获胜.则小姜可以获胜的最少回合是( )
盒空时她获胜.则小姜可以获胜的最少回合是( )
A.三回合B.四回合C.五回合D.六回合
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点.在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE.求直线BC与平面ABF所成角的大小,并求线段PH的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com