【题目】小姜同学有两个盒子
和
，最初盒子有6枚硬币，盒子是空的.在每一回合中，她可以将一枚硬币从盒移到盒，或者从盒移走
枚硬币，其中是盒中当前的硬币数.当盒空时她获胜.则小姜可以获胜的最少回合是( )
A.三回合B.四回合C.五回合D.六回合
【答案】B
【解析】
根据题意，前两回合只能是将一枚硬币从
盒移到
盒，从第三回合要分情况讨论，是将一枚硬币从盒移到盒，还是从盒移走
枚硬币，从而得到答案.
第一回合：将一枚硬币从盒移到盒，此时盒有5枚硬币，盒子有1枚硬币.
第二回合：将一枚硬币从盒移到盒，此时盒有4枚硬币，盒子有2枚硬币.
此时第三回合分为两种情况:
(1)第三回合：将一枚硬币从盒移到盒，此时盒有3枚硬币，盒子有3枚硬币.
第四回合：将三枚硬币从盒移走，此时盒有0枚硬币.
从而小姜获胜.
(2) 第三回合：将2枚硬币从盒移走，此时盒有1枚硬币.
第四回合：将一枚硬币从盒移到盒，此时盒有0枚硬币.
从而小姜获胜.
所以小姜要获胜，至少要四回合.
故选：B
科目：高中数学 来源： 题型：
【题目】已知圆
与抛物线
：
的准线交于
，
两点，且
．
（1）求抛物线的方程；
（2）若直线
：
与曲线交于
，
两点，且曲线上存在两点
，
关于直线对称，求实数
的取值范围及
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥
中，侧面
是边长为2的等边三角形且垂直于底面
，
，
，
是
的中点.
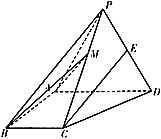
（1）求证：直线
平面
；
（2）点
在棱
上，且二面角
的余弦值为
，求直线
与底面所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下图是民航部门统计的某年春节期间：中国民航出入境航线方面TOP10出入境国家和地区的旅客量以及相比上年同期变化幅度的数据统计图表，根据图表，下面叙述不正确的是（ ）
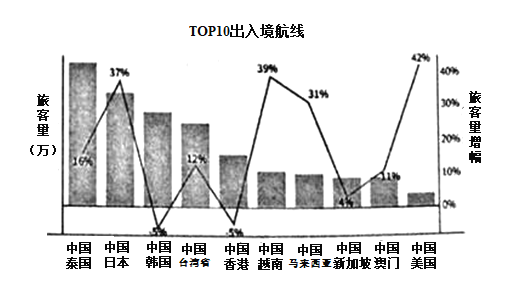
A.东南亚仍是人们出境旅游的首选
B.台湾和澳门均有超过一成的同比增长
C.越南和美国排在人们出境旅游选择的前两位
D.中-韩航线虽依然位列出入境国家和地区第三甲，但旅客量却较去年出现负增长
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4—4：坐标系与参数方程
在直角坐标系xOy中，设倾斜角为α的直线l：
（t为参数）与曲线C：
（θ为参数）相交于不同的两点A，B．
（Ⅰ）若α＝
，求线段AB中点M的坐标；
（Ⅱ）若｜PA｜·｜PB｜＝｜OP｜
，其中P（2，
），求直线l的斜率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
两点分别在
轴和
轴上运动，且
，若动点
满足
.
（1）求出动点
的轨迹
的标准方程；
（2）设动直线
与曲线有且仅有一个公共点，与圆
相交于两点
（两点均不在坐标轴上），求直线
的斜率之积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知正六棱锥
的底面边长为
，高为
．现从该棱锥的
个顶点中随机选取
个点构成三角形，设随机变量
表示所得三角形的面积.
（1）求概率
的值；
（2）求的分布列，并求其数学期望
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
