
已知一个袋子里有形状一样仅颜色不同的6个小球,其中白球2个,黑球4个. 现从中随机取球,每次只取一球.
(1)若每次取球后都放回袋中,求事件“连续取球四次,至少取得两次白球”的概率;
(2)若每次取球后都不放回袋中,且规定取完所有白球或取球次数达到五次就终止游戏,记游戏结束时一共取球X次,求随机变量X的分布列与期望
(1) ;
;
(2)随机变量X的分布列为:
X | 2 | 3 | 4 | 5 |
P |
|
|
|
|
随机变量X的期望为: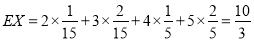 .
.
【解析】
试题分析:(1)由已知记事件 表示“第i次取到白球”(
表示“第i次取到白球”(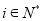 ),事件
),事件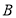 表示“连续取球四次,至少取得两次白球”,则:
表示“连续取球四次,至少取得两次白球”,则: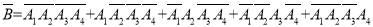 .利用相互独立事件同时发生的概率积公式进行计算;或者,由于每次取球后都放回袋中,所以每次取得白球的概率相同,记随机变量
.利用相互独立事件同时发生的概率积公式进行计算;或者,由于每次取球后都放回袋中,所以每次取得白球的概率相同,记随机变量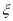 表示连续取球四次,取得白球的次数,则
表示连续取球四次,取得白球的次数,则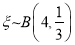 ,再利用
,再利用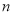 次独立重复试验某事件恰有
次独立重复试验某事件恰有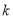 发生的概率公式
发生的概率公式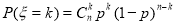 进行计算;(2)首先得到随机变量X的所有取值分别为2,3,4,5,然后利用古典概率公式计算出随机变量X取每一个值时所对应的概率,从而可得随机变量X的分布列与期望,注意:每次取球后都不放回袋中.
进行计算;(2)首先得到随机变量X的所有取值分别为2,3,4,5,然后利用古典概率公式计算出随机变量X取每一个值时所对应的概率,从而可得随机变量X的分布列与期望,注意:每次取球后都不放回袋中.
试题解析:(1)记事件 表示“第i次取到白球”(
表示“第i次取到白球”(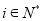 ),事件
),事件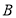 表示“连续取球四次,至少取得两次白球”,则:
表示“连续取球四次,至少取得两次白球”,则: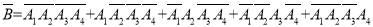 . 2分
. 2分
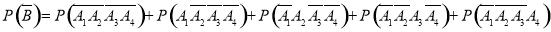
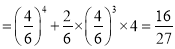 4分
4分
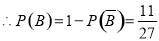 5分
5分
或者:记随机变量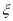 表示连续取球四次,取得白球的次数. 易知
表示连续取球四次,取得白球的次数. 易知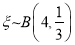 2分
2分
则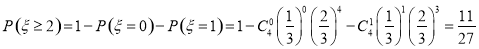 5分
5分
(2)易知:随机变量X的取值分别为2,3,4,5 6分
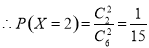 ,
, 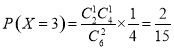
 ,
, 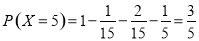 10分
10分
∴随机变量X的分布列为:
X | 2 | 3 | 4 | 5 |
P |
|
|
|
|
∴随机变量X的期望为: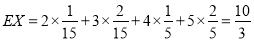 12分
12分
考点:1.相互独立事件同时发生的概率积公式;2.古典概型.3.分布列与数学期望.


科目:高中数学 来源:2015届江西省高三上学期第三次考试文科数学试卷(解析版) 题型:选择题
设集合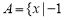 ≤x≤2},B=
≤x≤2},B=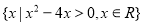 ,则
,则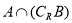 =
=
A.[1,2] B.[0,2] C.[1,4] D.[0,4]
查看答案和解析>>
科目:高中数学 来源:2015届江苏省苏州市高三上学期期中测试数学试卷(解析版) 题型:解答题
(本小题满分10分)在如图所示的多面体中,四边形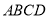 为正方形,四边形
为正方形,四边形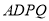 是直角梯形,
是直角梯形,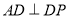 ,
,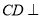 平面
平面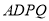 ,
,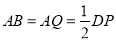 .
.

(1)求证: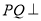 平面
平面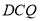 ;
;
(2)求平面 与平面
与平面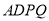 所成的锐二面角的大小.
所成的锐二面角的大小.
查看答案和解析>>
科目:高中数学 来源:2015届广东省深圳市高三上学期第一次五校联考理科数学试卷(解析版) 题型:填空题
已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题,其中所有正确命题的序号是___________.
①若m∥β,n∥β,m、n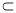 α,则α∥β .
α,则α∥β .
②若α⊥γ,β⊥γ,α∩β=m,n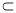 γ,则m⊥n .
γ,则m⊥n .
③若m⊥α,α⊥β,m∥n,则n∥β .
④若n∥α,n∥β,α∩β=m,那么m∥n .
查看答案和解析>>
科目:高中数学 来源:2015届广东省深圳市高三上学期第一次五校联考理科数学试卷(解析版) 题型:选择题
一个多面体的三视图如图所示,则该多面体的体积为( )
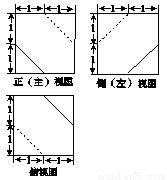
A.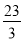 B.
B. C.
C.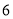 D.
D. 
查看答案和解析>>
科目:高中数学 来源:2015届广东省深圳市高三上学期第一次五校联考文科数学试卷(解析版) 题型:选择题
已知直线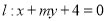 ,若曲线
,若曲线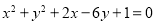 上存在两点P、Q关于直线
上存在两点P、Q关于直线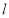 对称,
对称,
则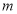 的值为
的值为
A.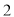 B.
B.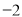 C.
C.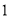 D.
D.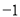
查看答案和解析>>
科目:高中数学 来源:2015届广东省高三上学期暑假联考文科数学试卷(解析版) 题型:选择题
已知变量 ,
, 满足约束条件
满足约束条件 ,目标函数
,目标函数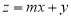 仅在点
仅在点 处取得最小值,则
处取得最小值,则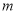 的取值范围是( )
的取值范围是( )
A.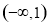 B.
B.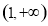 C.
C.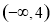 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com