
 | A规格 | B规格 | C规格 |
| 第一种钢板 | 2 | 1 | 1 |
| 第二种钢板 | 1 | 2 | 3 |
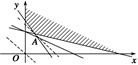 约束条件为:
约束条件为: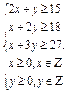
 可使z取最小,由于
可使z取最小,由于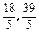 都不是整数,而最优解(x,y)中,x,y必须都是整数,可行域内点A
都不是整数,而最优解(x,y)中,x,y必须都是整数,可行域内点A 不是最优解;
不是最优解; 点距离最近的直线是x+y=12,经过的整点是B(3,9)和C(4,8),它们都是最优解.
点距离最近的直线是x+y=12,经过的整点是B(3,9)和C(4,8),它们都是最优解.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 甲 | 乙 | 丙 |
| 维生素A(单位/千克) | 400 | 600 | 400 |
| 维生素B(单位/千克) | 800 | 200 | 400 |
| 成本(元/千克) | 7 | 6 | 5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.99.75% | B.99.65% | C.94.85% | D.95.90% |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
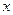 的实系数方程
的实系数方程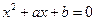 有两个根,一个根在区间
有两个根,一个根在区间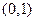 内,另一根在区间
内,另一根在区间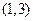 内,记点
内,记点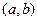 对应的区域为
对应的区域为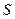 .
.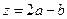 ,求
,求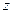 的取值范围;
的取值范围;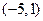 的一束光线,射到
的一束光线,射到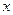 轴被反射后经过区域
轴被反射后经过区域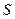 ,求反射光线所在直线
,求反射光线所在直线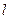 经过区域
经过区域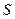 内的整点(即横纵坐标为整数的点)时直线
内的整点(即横纵坐标为整数的点)时直线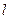 的方程.
的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 在平面直角坐标系中,有两个区域M、N,M是由三个不等式y≥0、y≤x和y≤2-x确定的;N是随t变化的区域,它由不等式t≤x≤t+1(0≤t≤1)所确定.设M、N的公共部分的面积为f(t),则f(t)等于
在平面直角坐标系中,有两个区域M、N,M是由三个不等式y≥0、y≤x和y≤2-x确定的;N是随t变化的区域,它由不等式t≤x≤t+1(0≤t≤1)所确定.设M、N的公共部分的面积为f(t),则f(t)等于A.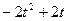 | B.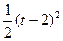 |
C.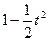 | D.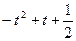 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com