
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 首先分析题目求在面积为S的△ABC的边AB上任取一点P,则△PBC的面积小于1的概率,即可考虑画图求解的方法,然后根据图形分析出基本的事件空间与事件的几何度量是什么.再根据几何关系求解出它们的比例即可.
解答 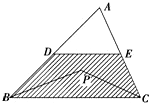 解:记事件A={△PBC的面积小于 1},
解:记事件A={△PBC的面积小于 1},
基本事件空间是三角形ABC的面积,(如图)
事件A的几何度量为图中阴影部分的面积(DE是三角形的中位线),
因为阴影部分的面积是整个三角形面积的$\frac{3}{4}$,
所以P(A)=$\frac{3}{4}$.
故选:D.
点评 本题考查了几何概型,解答此题的关键在于明确测度比是面积比.对于几何概型常见的测度是长度之比,面积之比,体积之比,角度之比,要根据题意合理的判断和选择是哪一种测度进行求解.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
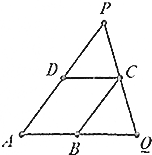 某小区现有一块草坪ABCD呈平行四边形形状,AB=3,AD=2,∠BAD=60°,为了改善居民的生活环境,决定将原草坪扩建成三角形PAQ形状,点A,D,P共线,Q,C,P共线,A,B,Q共线,设AP=x,BQ=y.
某小区现有一块草坪ABCD呈平行四边形形状,AB=3,AD=2,∠BAD=60°,为了改善居民的生活环境,决定将原草坪扩建成三角形PAQ形状,点A,D,P共线,Q,C,P共线,A,B,Q共线,设AP=x,BQ=y.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
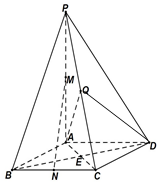 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,E为AC与BD的交点,PA⊥平面ABCD,M为PA中点,N为BC中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,E为AC与BD的交点,PA⊥平面ABCD,M为PA中点,N为BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com