
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
���� ���ݡ��ȷ������С��Ķ��壬������һ�жϿɵô𰸣�
��� �⣺��{an}�ǵȷ������У���an2-an-12=p��pΪ�������õ�{an2}Ϊ������a12������Ϊp�ĵȲ����У�
��{an2}�ǵȲ����У��ʢ���ȷ���ڲ���ȷ��
����{��-1��n}��an2-an-12=[��-1��n]2-[��-1��n-1]2=0��
��{��-1��n}�ǵȷ������У��ʢ���ȷ��
����{an}�е����оٳ����ǣ�a1��a2������ak������a2k����
����{akn}�е����оٳ����ǣ�ak��a2k������a3k������
�ߣ�ak+12-ak2��=��ak+22-ak+12��=��ak+32-ak+22��=��=��a2k2-a2k-12��=p
�ࣨak+12-ak2��+��ak+22-ak+12��+��ak+32-ak+22��+��+��a2k2-a2k-12��=kp
�ࣨakn+12-akn2��=kp
��{akn}��k��N*��kΪ�������ǵȷ������У��ʢ���ȷ��
��ѡ��B��
���� ���⿼��ѧ��������õȲ����е����ʼ��¶���ȷ������л�����ֵ����һ���е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{6}$ | B�� | 2 | C�� | 3 | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{2}$ | B�� | -1 | C�� | -5 | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
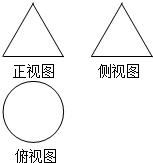 ��ͼ��ʾ��һ���ռ伸���������ͼ�Ͳ���ͼ���DZ߳�Ϊ4�ĵȱ������Σ�����ͼ��һ��Բ����ô�����Ϊ��������
��ͼ��ʾ��һ���ռ伸���������ͼ�Ͳ���ͼ���DZ߳�Ϊ4�ĵȱ������Σ�����ͼ��һ��Բ����ô�����Ϊ��������| A�� | $\frac{{4\sqrt{3}}}{3}��$ | B�� | $\frac{{8\sqrt{3}}}{3}��$ | C�� | $\frac{{\sqrt{3}}}{2}��$ | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com