
分析 (1)由f(x)是奇函数,可得f(-x)=-f(x),解出b,c,再利用基本不等式的性质可得a.
(2)由2an+1=f(an)-an(n∈N*),可得an+1与an的关系,令bn=$\frac{{{a_n}-1}}{{{a_n}+1}}$,利用递推关系即可证明bn+1=bn2.
(3)由a1=2>0,可得${b_{n+1}}={(\frac{{{a_n}-1}}{{{a_n}+1}})^2}={b_n}^2>0$.取对数得$lg{b_{n+1}}=lg{b_n}^2=2lg{b_n}$.利用等比数列的通项公式即可得出.
解答 解:(1)∵f(x)是奇函数,∴有f(-x)=-f(x),即$\frac{{a{x^2}-bx+1}}{-x+c}=-\frac{{a{x^2}+bx+1}}{x+c}$.
整理得(b-ac)x2=c对x≠0恒成立.∴有$\left\{\begin{array}{l}b=ac\\ c=0\end{array}\right.$,∴b=c=0.
∴$f(x)=\frac{{a{x^2}+1}}{x}$.
∵a>0,∴当x>0时,∴$f(x)=ax+\frac{1}{x}≥2\sqrt{a}=2\sqrt{2}$,∴a=2.∴$f(x)=\frac{{2{x^2}+1}}{x}$.
(2)证明:$2{a_{n+1}}=f({a_n})-{a_n}=\frac{{2{a_n}^2+1}}{a_n}-{a_n}=2{a_n}+\frac{1}{a_n}-{a_n}={a_n}+\frac{1}{a_n}$.
∵${b_n}=\frac{{{a_n}-1}}{{{a_n}+1}}$,
∴${b_{n+1}}=\frac{{{a_{n+1}}-1}}{{{a_{n+1}}+1}}=2\frac{{2{a_{n+1}}-2}}{{{a_{n+1}}+2}}=\frac{{{a_n}+\frac{1}{a_n}-2}}{{{a_n}+\frac{1}{a_n}+2}}=\frac{{{a_n}^2-2{a_n}+1}}{{{a_n}^2+2{a_n}+1}}$=$\frac{{{{({a_n}-1)}^2}}}{{{{({a_n}+1)}^2}}}={(\frac{{{a_n}-1}}{{{a_n}+1}})^2}={b_n}^2$.
(3)∵a1=2>0,∴${b_{n+1}}={(\frac{{{a_n}-1}}{{{a_n}+1}})^2}={b_n}^2>0$.取对数得$lg{b_{n+1}}=lg{b_n}^2=2lg{b_n}$.
由${b_n}=\frac{{{a_n}-1}}{{{a_n}+1}}$得bn≠1,∴lgbn≠0.∴有$\frac{{lg{b_{n+1}}}}{{lg{b_n}}}=2$为常数.
∴数列$\{\frac{{lg{b_{n+1}}}}{{lg{b_n}}}\}$为等比数列.
∵${b_1}=\frac{{{a_1}-1}}{{{a_1}+1}}=\frac{2-1}{2+1}=\frac{1}{3}$,∴$lg{b_n}=(lg\frac{1}{3})•{2^{n-1}}={2^{n-1}}lg\frac{1}{3}=lg{(\frac{1}{3})^{2n-1}}$.
∴${b_n}=(\frac{1}{3}){2^{n-1}}$.
点评 本题考查了数列的递推关系、等比数列的通项公式、对数的运算性质、函数的奇偶性,考查了推理能力与计算能力,属于中档题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:解答题
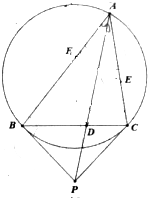 设锐角△ABC的外接圆为圆Γ,过点B,C作圆Γ的两条切线交于点P,链接AP与BC交于点D,点E,F分别在边AC,AB上,使得DE∥BA,DF∥CA.证明:F,B,C,E四点共圆.
设锐角△ABC的外接圆为圆Γ,过点B,C作圆Γ的两条切线交于点P,链接AP与BC交于点D,点E,F分别在边AC,AB上,使得DE∥BA,DF∥CA.证明:F,B,C,E四点共圆.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
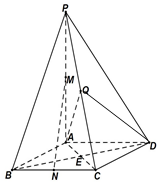 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,E为AC与BD的交点,PA⊥平面ABCD,M为PA中点,N为BC中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,E为AC与BD的交点,PA⊥平面ABCD,M为PA中点,N为BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com