
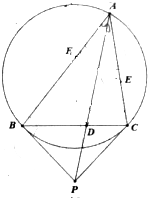
 设锐角△ABC的外接圆为圆Γ,过点B,C作圆Γ的两条切线交于点P,链接AP与BC交于点D,点E,F分别在边AC,AB上,使得DE∥BA,DF∥CA.证明:F,B,C,E四点共圆.
设锐角△ABC的外接圆为圆Γ,过点B,C作圆Γ的两条切线交于点P,链接AP与BC交于点D,点E,F分别在边AC,AB上,使得DE∥BA,DF∥CA.证明:F,B,C,E四点共圆. 分析 欲证明F,B,C,E四点共圆,只要证明AF•AB=AE•AC,进而转化为证明$\frac{BD}{CD}$=$\frac{A{B}^{2}}{A{C}^{2}}$.
解答 证明:欲证明F,B,C,E四点共圆,只要证明AF•AB=AE•AC.
∵DE∥BA,DF∥CA,
∴AF=DE=AB$•\frac{CD}{BC}$,AE=DF=AC•$\frac{BD}{BC}$,
于是只要证明$\frac{BD}{CD}$=$\frac{A{B}^{2}}{A{C}^{2}}$.
注意到∠ABP=180°-∠ACB,∠ACP=180°-∠ABC,
则$\frac{BD}{CD}$=$\frac{{S}_{△ABP}}{{S}_{△ACP}}$=$\frac{\frac{1}{2}AB•BP•sin∠ABP}{\frac{1}{2}AC•CP•sin∠ACP}$=$\frac{ABsin(180°-∠ACB)}{ACsin(180°-∠ABC)}$=$\frac{A{B}^{2}}{A{C}^{2}}$.得证,
∴F,B,C,E四点共圆.
点评 本题考查四点共圆的证明,考查三角形面积的计算,正确转化是关键.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 和a的取值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com