
分析 (Ⅰ)利用已知条件求出b,通过离心率以及a、b、c关系,求出a,即可求椭圆的方程;
(Ⅱ)求出A设出B,得到直线方程,求出P的坐标,计算下来的数量积,推出结果即可.
解答 解:(Ⅰ)∵$e=\sqrt{1-\frac{b^2}{a^2}}=\frac{{\sqrt{2}}}{2}$,b=1,∴a2=2,b2=1,∴椭圆的方程为$\frac{x^2}{2}+{y^2}=1$.…(4分)
(Ⅱ)由(1)可知点$A(-\sqrt{2},0)$,设B(x0,y0),则$l:y=\frac{y_0}{{{x_0}+\sqrt{2}}}(x+\sqrt{2})$.…(6分)
令$x=\sqrt{2}$,解得$y=\frac{{2\sqrt{2}{y_0}}}{{{x_0}+\sqrt{2}}}$,即$P(\sqrt{2},\frac{{2\sqrt{2}{y_0}}}{{{x_0}+\sqrt{2}}})$,…(8分)
∴$\overrightarrow{OB}•\overrightarrow{OP}=({x_0},{y_0})•(\sqrt{2},\frac{{2\sqrt{2}{y_0}}}{{{x_0}+\sqrt{2}}})=\frac{{\sqrt{2}({x_0}^2+2{y_0}^2)+2{x_0}}}{{{x_0}+\sqrt{2}}}$,…(10分)
又∵B(x0,y0)在椭圆上,则${x_0}^2+2{y_0}^2=2$,∴$\overrightarrow{OB}•\overrightarrow{OP}=2$.…(12分)
点评 本题考查椭圆的方程的求法,向量在椭圆中的应用,直线与椭圆的位置关系,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{{x^2}+1}}<1$ | B. | x2+1≥2|x| | C. | lg(x2+1)≥lg2x | D. | $\frac{4x}{{{x^2}+4}}$≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
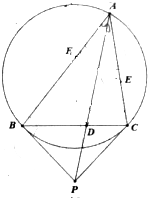 设锐角△ABC的外接圆为圆Γ,过点B,C作圆Γ的两条切线交于点P,链接AP与BC交于点D,点E,F分别在边AC,AB上,使得DE∥BA,DF∥CA.证明:F,B,C,E四点共圆.
设锐角△ABC的外接圆为圆Γ,过点B,C作圆Γ的两条切线交于点P,链接AP与BC交于点D,点E,F分别在边AC,AB上,使得DE∥BA,DF∥CA.证明:F,B,C,E四点共圆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com