
分析 ①先通过给x赋值1得到展开式的各项系数和;再利用二项展开式的通项公式求出第r+1项,令x的指数为-3得到展开式中$\frac{1}{{x}^{3}}$的系数.
②根据相关指数R2的性质进行判断,
③根据函数奇偶性和对称性的性质进行判断,
④根据正态分布的概率关系进行判断.
解答 解:①令x=1得展开式的各项系数和为2n
∴2n=128解得n=7
∴${(3x-\frac{1}{\root{3}{{x}^{2}}})}^{n}$=${(3x-\frac{1}{\root{3}{{x}^{2}}})}^{7}$展开式的通项为${T}_{r+1}={C}_{7}^{r}{(3x)}^{7-r\;}{(-\frac{1}{\root{3}{{x}^{2}}})}^{r}$=${(-1)}^{r}{3}^{7-r}{C}_{7}^{r}{x}^{7-\frac{5r}{3}}$
令$7-\frac{5r}{3}=-3$解得r=6
∴展开式中$\frac{1}{{x}^{3}}$的系数为3C76=21,故①错误,
②在线性回归模型中,R2表示解释变量对预报变量的贡献率,R2越接近于1,表示解释变量和预报变量的线性相关关系越强;
说明模型的拟合效果越好;故②正确,
③若f(x)是定义在R上的奇函数,且满足f(x+2)=-f(x),
则f(x+2)=-f(x),
即f(x+1)=-f(x-1)=f(1-x),则函数f(x)的图象关于x=1对称;故③正确,
④已知随机变量ξ服从正态分布N(1,σ2),P(ξ≤4)=0.79,则P(ξ≤-2)=P(ξ>4)=1-P(ξ≤4)=1-0.79=0.21,故④正确;
故答案为:③④
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,但难度不大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
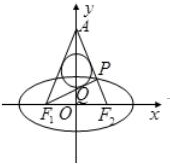 如图,焦点在x轴上的椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{3}$=1(a>0)的左、右焦点分别为F1,F2,P是椭圆上位于第一象限内的一点,且直线F2P与y轴的正半轴交于A点,△APF1的内切圆在边PF1上的切点为Q,若|F1Q|=4,则a=4.
如图,焦点在x轴上的椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{3}$=1(a>0)的左、右焦点分别为F1,F2,P是椭圆上位于第一象限内的一点,且直线F2P与y轴的正半轴交于A点,△APF1的内切圆在边PF1上的切点为Q,若|F1Q|=4,则a=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com