
分析 (1)由过点P(1,-2)的直线l的倾斜角为45°,可得直线l的参数方程.曲线C的极坐标方程为ρsin2θ=2cosθ,即ρ2sin2θ=2ρcosθ,利用互化公式可得直角坐标方程.
(2)把直线l的参数方程代入抛物线方程可得:t2-6$\sqrt{2}$t+4=0.利用根与系数的关系、参数的几何意义即可得出.
解答 解:(1)∵过点P(1,-2)的直线l的倾斜角为45°,可得直线l的参数方程为:$\left\{\begin{array}{l}{x=1+\frac{\sqrt{2}}{2}t}\\{y=-2+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数).
曲线C的极坐标方程为ρsin2θ=2cosθ,即ρ2sin2θ=2ρcosθ,可得直角坐标方程:y2=2x.
(2)把直线l的参数方程代入抛物线方程可得:t2-6$\sqrt{2}$t+4=0.
∴t1t2=4.
∴|PA|•|PB|=|t1t2|=4.
点评 本题考查了极坐标与直角坐标方程的互化公式、直线的参数方程及其应用,考查了推理能力与计算能力,属于中档题.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1或-3 | C. | 3 | D. | -1或3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$ | B. | $\overrightarrow{AB}$=$\overrightarrow{OA}$-$\overrightarrow{OB}$ | C. | $\overrightarrow{AB}$-$\overrightarrow{BA}$=$\overrightarrow 0$ | D. | $\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CD}$=$\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
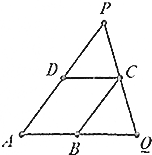 某小区现有一块草坪ABCD呈平行四边形形状,AB=3,AD=2,∠BAD=60°,为了改善居民的生活环境,决定将原草坪扩建成三角形PAQ形状,点A,D,P共线,Q,C,P共线,A,B,Q共线,设AP=x,BQ=y.
某小区现有一块草坪ABCD呈平行四边形形状,AB=3,AD=2,∠BAD=60°,为了改善居民的生活环境,决定将原草坪扩建成三角形PAQ形状,点A,D,P共线,Q,C,P共线,A,B,Q共线,设AP=x,BQ=y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com