
分析 不妨设方程x4-15x3+kx2+175x-1992=0的四个根为x1,x2,x3,x4,且x1x2=24;从而由x4-15x3+kx2+175x-1992=(x-x1)(x-x2)(x-x3)(x-x4)=(x2-(x1+x2)x+x1x2)(x2-(x3+x4)x+x3x4)可得x1x2x3x4=-1992,x1+x2+x3+x4=15,83(x1+x2)-24(x3+x4)=175,从而求k.
解答 解:不妨设方程x4-15x3+kx2+175x-1992=0的四个根为x1,x2,x3,x4,且x1x2=24;
则x4-15x3+kx2+175x-1992=(x-x1)(x-x2)(x-x3)(x-x4)
=(x2-(x1+x2)x+x1x2)(x2-(x3+x4)x+x3x4);
故x1x2x3x4=-1992,
故x3x4=-$\frac{1992}{24}$=-83;
故(x2-(x1+x2)x+24)(x2-(x3+x4)x-83)
则x1+x2+x3+x4=15,
83(x1+x2)-24(x3+x4)=175,
联立方程解得,
x1+x2=5,x3+x4=10;
故k=(x1+x2)(x3+x4)+24-83=50+24-83=-9.
点评 本题考查了多项式的化简与运算,属于中档题.


科目:高中数学 来源:2017届河北沧州一中高三上第七周周测数学试卷(解析版) 题型:选择题
已知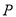 是
是 所在平面内一点且
所在平面内一点且 ,现将一粒黄豆随机撕在
,现将一粒黄豆随机撕在 内,则黄豆落在
内,则黄豆落在 内的概率是( )
内的概率是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com