
【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
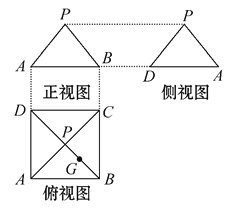
(1)根据三视图,画出该几何体的直观图.
(2)在直观图中,①证明:PD∥平面AGC;
②证明:平面PBD⊥平面AGC.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)根据三视图,可得该几何体为正四棱锥![]() ,正方形
,正方形![]() 的边长为2,正四棱锥的高为
的边长为2,正四棱锥的高为![]() ,由此可得该几何体的直观图.
,由此可得该几何体的直观图.
(Ⅱ)①在直观图中,设正方形![]() 的中心为
的中心为![]() ,利用三角形的中位线证明
,利用三角形的中位线证明![]() .再由直线和平面平行的判定定理证得
.再由直线和平面平行的判定定理证得![]() 面
面![]() .
.
②连接![]() ,则
,则![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,即可求此几何体的侧面积.
,即可求此几何体的侧面积.
试题解析:(1)该几何体的直观图如图所示.
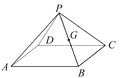
(2)如图,①连接AC,BD交于点O,连接OG,
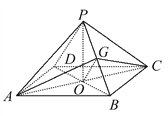
因为G为PB的中点,O为BD的中点,所以OG∥PD,又OG平面AGC,PD平面AGC,所以PD∥平面AGC.
②连接PO,由三视图,PO⊥平面ABCD,所以AO⊥PO.又AO⊥BO,BO∩PO=O,所以AO⊥平面PBD,因为AO平面AGC,所以平面PBD⊥平面AGC.


科目:高中数学 来源: 题型:
【题目】有一块扇形铁皮OAB,∠AOB=60°,OA=72cm,要剪下来一个扇环形ABCD,作圆台容器的侧面,并且在余下的扇形OCD内能剪下一块与其相切的圆形使它恰好作圆台容器的下底面(大底面).试求:
(1)AD应取多长?
(2)容器的容积为多大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,下图![]() 为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含
为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含![]() 个小正方形.
个小正方形.
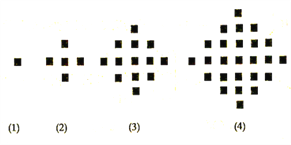
(1)求出![]() ;
;
(2)利用合情推理的“归纳推理思想”归纳出![]() 与
与![]() 的关系式,
的关系式,
(3)根据你得到的关系式求![]() 的表达式
的表达式
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示是某企业2010年至2016年污水净化量(单位: 吨)的折线图.
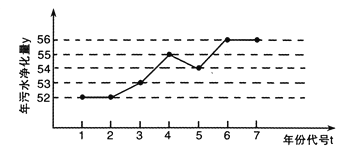
注: 年份代码1-7分别对应年份2010-2016.
(1)由折线图看出,可用线性回归模型拟合![]() 和
和![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程,预测
的回归方程,预测![]() 年该企业污水净化量;
年该企业污水净化量;
(3)请用数据说明回归方程预报的效果.
附注: 参考数据:![]() ;
;
参考公式:相关系数 ,回归方程
,回归方程![]() 中斜率和截距的最小;
中斜率和截距的最小;
二乘法估汁公式分别为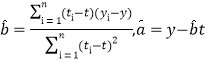 ;
;
反映回归效果的公式为: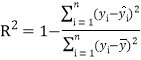 ,其中
,其中![]() 越接近于
越接近于![]() ,表示回归的效果越好.
,表示回归的效果越好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品上市30天内每件的销售价格![]() 元与时间
元与时间![]() 天函数关系是
天函数关系是
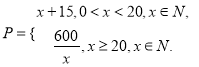 该商品的日销售量
该商品的日销售量![]() 件与时间
件与时间![]() 天函数关系是
天函数关系是
![]() .(1)求该商品上市第20天的日销售金额;
.(1)求该商品上市第20天的日销售金额;
(2)求这个商品的日销售金额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为常数,
为常数,![]() ).(Ⅰ)求函数
).(Ⅰ)求函数![]() 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立?如果存在,求
恒成立?如果存在,求![]() 的取值范围;如果不存在,请说明理由(其中
的取值范围;如果不存在,请说明理由(其中![]() 是自然对数的底数,
是自然对数的底数,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】做投掷2个骰子试验,用(x,y)表示点P的坐标,其中x表示第1个骰子出现的点数,y表示第2个骰子出现的点数.
(1)求点P在直线y=x上的概率.
(2)求点P不在直线y=x+1上的概率.
(3)求点P的坐标(x,y)满足16<x2+y2≤25的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com