练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    平面α∥平面β，点A, C∈α, B, D∈β，则直线AC∥直线BD的充要条件是

        A．AB∥CD                       B．AD∥CB

        C．AB与CD相交              D．A, B, C, D四点共面


    D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    为了让学生了解更多“奥运会”知识，某中学举行了一次“奥运知识竞赛”，共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计．请你根据尚未完成并有局部污损的频率分布表，解答下列问题：

    (1)若用系统抽样的方法抽取50个样本，现将所有学生随机地编号为000，001，002，…799， 试写出第二组第一位学生的编号；

    (2)填充频率分布表的空格(将答案直接填在表格内) ，并作出频率分布直方图；

    (3)若成绩在85.5~95.5分的学生为二等奖，问参赛学生中获得二等奖的约多少人？

    分组

    频数

    频率

    60.5~70.5

    0.16

    70.5~80.5

    10

    80.5~90.5

    18

    0.36

    90.5~100.5

    合计

    50

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设集合A＝(―∞, ―2]∪[3, ＋∞)，关于x的不等式(x－2a)·(x＋a)＞0的解集为B（其中a＜0).

    （1）求集合B；

    （2）设p: x∈A, q: x∈B，且Øp是Øq的充分不必要条件，求a的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝|log3x|，若0＜m＜n且f(m)＝f(n)，则2m＋n的取值范围为             。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝2cos2＋sinwx＋a的图象上相邻两对称轴的距离为.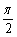

    （1）若x∈R，求f(x)的递增区间；

    （2）若x∈[0, 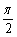]时，f(x)的最大值为4，求a的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知双曲线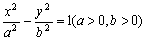的左焦点为F1，左、右顶点分别为A1、A2，

    P为双曲线上任意一点，则分别以线段PF1，A1A2为直径的两个圆的位置关系为

        A．相交         B．相切         C．相离         D．以上情况都有可能

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知两曲线参数方程分别为

    （0≤θ＜π）和(t∈R)，它们的交点坐标为                    。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正方形OABC的四个顶点O(0, 0), A(1, 0), B(1, 1), C(0, 1)，设u＝2xy, v＝x2－y2，是一个由平面xOy到平面uOv上的变换，则正方形OABC在这个变换下的图形是

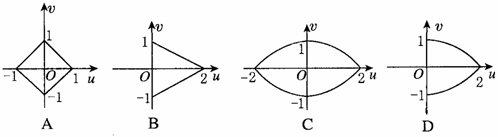
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下面四图都是在同一坐标系中某三次函数及其导函数的图像，其中一定不正确的序号是(　　)

    A．①②     B．③④      C．①③            D．①④

    查看答案和解析>>

    同步练习册答案