
���� ��1������C�IJ�������Ϊ$\left\{{\begin{array}{l}{x=2cos��}\\{y=sin��}\end{array}}$������Ϊ������������ƽ����ϵ�ɵã����� C��ֱ������ϵ�µ���ͨ���̣����仯Ϊ�����귽��Ϊ$\frac{{{��^2}{{cos}^2}��}}{4}+{��^2}{sin^2}��=1$���ֱ����$��=\frac{��}{4}$��$��=-\frac{��}{4}$���ɵ�|OA|��|OB|��$��AOB=\frac{��}{2}$������ֱ��������������㹫ʽ�ɵá�AOB�������
��2����l�ļ����귽�̻�Ϊֱ�����귽�̵�x-y-2=0������Բ��������������ɵó��������꣮
��� �⣺��1������C�IJ�������Ϊ$\left\{{\begin{array}{l}{x=2cos��}\\{y=sin��}\end{array}}$������Ϊ��������
����ƽ����ϵ�ɵã����� C��ֱ������ϵ�µ���ͨ����Ϊ$\frac{x^2}{4}+{y^2}=1$��
���仯Ϊ�����귽��Ϊ$\frac{{{��^2}{{cos}^2}��}}{4}+{��^2}{sin^2}��=1$��
�ֱ����$��=\frac{��}{4}$��$��=-\frac{��}{4}$����${|{OA}|^2}={|{OB}|^2}=\frac{8}{5}$��
��$��AOB=\frac{��}{2}$���ʡ�AOB�����$S=\frac{1}{2}|{OA}||{OB}|=\frac{4}{5}$��
��2����l�ļ����귽�̻�Ϊֱ�����귽�̣���x-y-2=0��
��������$\left\{{\begin{array}{l}{\frac{x^2}{4}+{y^2}=1}\\{x-y-2=0}\end{array}}\right.$�����x=2��y=0����$x=\frac{6}{5}��y=-\frac{4}{5}$��
������C��ֱ��l�Ľ�������Ϊ��2��0����$��{\frac{6}{5}��-\frac{4}{5}}��$��
���� ���⿼���˼����귽�̻�Ϊֱ�����귽�̡��������̻�Ϊ��ͨ���̡�ֱ������Բ�Ľ��㣬������������������������������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ��Į | ����Į | �ܼ� | |
| ����� | 68 | 42 | 110 |
| �ٿ����� | 20 | 38 | 58 |
| �ܼ� | 88 | 80 | 168 |
| P��K2��k�� | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 5.024 | 6.635 | 7.879 | 10.828 |
| A�� | ��Լ��99.9%�İ�����Ϊ����������˱���Į���й�ϵ | |
| B�� | ��Լ��99.9%�İ�����Ϊ����������˱���Į��û�й�ϵ | |
| C�� | ij�˰������ӣ���������Į�Ŀ�����Ϊ99.9% | |
| D�� | �������ӵ����д�Լ��99.9%�����Į |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
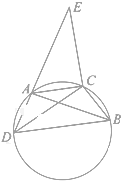 ��ͼ���ı���ADBC��Բ�ڽ��ı��Σ���CAB=��ADC���ӳ�DA��EʹBD=AE������EC��
��ͼ���ı���ADBC��Բ�ڽ��ı��Σ���CAB=��ADC���ӳ�DA��EʹBD=AE������EC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com