
分析 (1)求出函数的导数,通过解关于导函数的不等式,得到函数的单调性,结合零点存在定理证出结论即可;
(2)问题转化为证明x1+x2>2x0,根据m(x)在(x0,+∞)上递减,即证明m(m2)<m(2x0-x1),根据函数的单调性证明即可.
解答 证明:(1)F(x)=xlnx-$\frac{x}{{e}^{x}}$,定义域是(0,+∞),
F′(x)=1+lnx+$\frac{x-1}{{e}^{x}}$,
x>1时,F′(x)>0,∴F(x)在(1,+∞)递增,
又F(1)=-$\frac{1}{e}$<0,F(2)=2ln2-$\frac{2}{{e}^{2}}$>0,
而F(x)在(1,+∞)上连续,
根据零点存在定理可得:F(x)=0在区间(1,+∞)有且只有1个实根;
(2)0<x≤1时,f(x)=xlnx≤0,而g(x)=$\frac{x}{{e}^{x}}$>0,
故此时有f(x)<g(x),
由(1)得:F(x)在(1,+∞)递增,又x0为F(x)=0在(1,+∞)内的实根,
∴F(x0)=f(x0)-g(x0)=0,故1<x<x0时,即f(x)<g(x),
x>x0时,F(x)>0即f(x)>g(x),
∴m(x)=$\left\{\begin{array}{l}{xlnx,0<x{≤x}_{0}}\\{\frac{x}{{e}^{x}},x{>x}_{0}}\end{array}\right.$,
1<x<x0时,m(x)=xlnx,m′(x)=1+lnx>0,
∴m(x)在(1,x0)递增,
x>x0时,m(x)=$\frac{x}{{e}^{x}}$,m′(x)=$\frac{1-x}{{e}^{x}}$<0,
∴m(x)在(x0,+∞)递减,
若方程m(x)=c在(1,+∞)有两个不相等的实根x1,x2(x1<x2),
则满足x1∈(1,x0),x2∈(x0,+∞),
要证明$\frac{{x}_{1}+{x}_{2}}{2}$>x0,即证明x1+x2>2x0,即证明x2>2x0-x1>x0,
而m(x)在(x0,+∞)上递减,即证明m(m2)<m(2x0-x1),
∵m(x1)=m(x2),
即证明:m(x1)<m(2x0-x1),即证明:lnx1<$\frac{{2x}_{0}{-x}_{1}}{{e}^{{2x}_{0}{-x}_{1}}}$,x1∈(1,x0),
记h(x)=xlnx-$\frac{{2x}_{0}-x}{{e}^{{2x}_{0}-x}}$,x∈(1,x0),
由F(x0)=0得:x0lnx0=$\frac{{x}_{0}}{{e}^{{x}_{0}}}$,∴h(x0)=0,
h′(x)=1+lnx+$\frac{1}{{e}^{{2x}_{0}-x}}$-$\frac{{2x}_{0}-x}{{e}^{{2}_{0}-x}}$,
g(x)=$\frac{x}{{e}^{x}}$,g′(x)=$\frac{1-x}{{e}^{x}}$,
0<x<1时,g′(x)>0,x>1时,g′(x)<0,
故g(x)≤g(1)=$\frac{1}{e}$,
∴x>0时,0<g(x)≤$\frac{1}{e}$,
∵2x0-x>0,∴0<$\frac{{2x}_{0}-x}{{e}^{{2}_{0}-x}}$≤$\frac{1}{e}$,
∴h′(x)=1+lnx+$\frac{1}{{e}^{{2x}_{0}-x}}$-$\frac{{2x}_{0}-x}{{e}^{{2}_{0}-x}}$>1-$\frac{1}{e}$>0,
∴h(x)递增,从而1<x1<x0时,h(x)<h(x0)=0,
即lnx1<$\frac{{2x}_{0}{-x}_{1}}{{e}^{{2x}_{0}{-x}_{1}}}$,
故$\frac{{x}_{1}+{x}_{2}}{2}$>x0得证.
点评 本题考查了函数的单调性、最值问题,考查函数的零点存在定理,导数的应用,不等式的证明,是一道综合题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:解答题
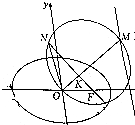 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,离心率为$\frac{\sqrt{2}}{2}$,且直线2x+y-3=0与椭圆C相切.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,离心率为$\frac{\sqrt{2}}{2}$,且直线2x+y-3=0与椭圆C相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $A_5^5$ | B. | $A_3^3•A_3^3$ | C. | $\frac{A_5^5}{A_3^3}$ | D. | $A_3^3$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com