
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据三角形(非直角三角形)的外心、内心、垂心和重心的向量表示与运算性质,对选项中的命题逐一进行分析、判断正误即可.
解答 解:对于①,点G是△ABC的重心,如图①所示,
所以$\overrightarrow{AG}$=$\frac{2}{3}$$\overrightarrow{AD}$=$\frac{2}{3}$×$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
同理$\overrightarrow{BG}$=$\frac{1}{3}$($\overrightarrow{BA}$+$\overrightarrow{BC}$),$\overrightarrow{CG}$=$\frac{1}{3}$($\overrightarrow{CB}$+$\overrightarrow{CA}$),
∴$\overrightarrow{AG}$+$\overrightarrow{BG}$+$\overrightarrow{CG}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$+$\overrightarrow{BA}$+$\overrightarrow{BC}$+$\overrightarrow{CB}$+$\overrightarrow{CA}$)=$\overrightarrow{0}$,
所以$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}$=$\overrightarrow{0}$,命题正确;
对于②,点O是△ABC的外心,如图②所示,
OA=OB=OC,
所以S△BOC:S△AOC:S△AOB═sin∠BOC:sin∠AOC:sin∠AOB=sin2A:sin2B:sin2C,
所以sin2A•$\overrightarrow{OA}$+sin2B•$\overrightarrow{OB}$+sin2C•$\overrightarrow{OC}$=$\overrightarrow{0}$,命题正确;
对于③,点I是△ABC的内心,如图所示,
所以S△BIC:S△AIC:S△AIB=a:b:c,所以a$\overrightarrow{IA}$+b$\overrightarrow{IB}$+c$\overrightarrow{IC}$=$\overrightarrow{0}$,命题正确;
对于④,点H是△ABC(非直角三角形)的垂心,如图所示,
所以S△BHC:S△AHC:S△ANB=tanA:tanB:tanC,
所以tanA•$\overrightarrow{HA}$+tanB•$\overrightarrow{HB}$+tanC•$\overrightarrow{HC}$=$\overrightarrow{0}$,命题正确.
综上,以上正确的命题有4个.
故选:D.
点评 本题考查了非直角三角形的外心、内心、垂心和重心的向量表示与性质的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,$-\frac{2π}{3}$) | B. | (2,$-\frac{π}{3}$) | C. | (2,$\frac{π}{3}$) | D. | (2,$\frac{2π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
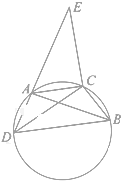 如图,四边形ADBC是圆内接四边形,∠CAB=∠ADC.延长DA到E使BD=AE,连结EC.
如图,四边形ADBC是圆内接四边形,∠CAB=∠ADC.延长DA到E使BD=AE,连结EC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方体AC1中,已知O为AC与BD的交点,M为DD1的中点.
如图,正方体AC1中,已知O为AC与BD的交点,M为DD1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com