Question

5．如图，正方体AC₁中，已知O为AC与BD的交点，M为DD₁的中点．
（1）求异面直线B₁O与AM所成角的大小．
（2）求二面角B₁-MA-C的正切值．

Answer 1

分析 （1）先证B₁O⊥MAC，证明直线与平面垂直，关键要找到两条相交直线与之都垂直．有时候题目中没有现成的直线与直线垂直，需要我们先通过直线与平面垂直去转化一下，如欲证B₁O⊥AC，可以先证明AC⊥平面BB₁O，从而B₁O⊥AM；
（2）二面角的度量关键在于找出它的平面角，构造平面角常用的方法就是三垂线法．

解答 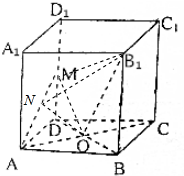解：（1）∵BB₁⊥平面ABCD，OB⊥AC，
∴B₁O⊥AC．设棱长为2
连接MO、MB₁，则MO=$\sqrt{3}$，B₁O=$\sqrt{6}$，MB₁=3．
∵MO²+B₁O²=MB₁²，∴∠MOB₁=90°．
∴B₁O⊥MO．
∵MO∩AC=O，∴B₁O⊥平面MAC．
∴B₁O⊥AM，
∴异面直线B₁O与AM所成角为90°；
（2）作ON⊥AM于点N，连接B₁N．
∵B₁O⊥平面MAC，∴AM⊥平面B₁ON．
∴B₁N⊥AM．
∴∠B₁NO就是二面角B₁-MA-C的平面角．
∵AM=$\sqrt{5}$，CM=$\sqrt{5}$，∴AM=CM．
又O为AC的中点，∴OM⊥AC．则ON=OAsin∠MAO=$\frac{\sqrt{6}}{\sqrt{5}}$．
在Rt△B₁ON中，tan∠B₁NO=$\frac{{B}_{1}O}{ON}$=$\sqrt{5}$，
∴∠B₁NO=arctan$\sqrt{5}$，即所求二面角的大小为arctan$\sqrt{5}$．

点评 证明直线与直线垂直常用的方法有勾股定理、通过直线与平面垂直转化，三垂线定理，其中在立体几何证明垂直的问题中，三垂线定理应用很多，本题的两问都是三垂线定理的应用实例．