

| A. | -$\frac{1}{2}$ | B. | -$\frac{{\sqrt{3}}}{2}$ | C. | -$\frac{{\sqrt{2}}}{2}$ | D. | -$\frac{1}{3}$ |
分析 设OP直线的倾斜角为α,由题意可得cosα=$\frac{\sqrt{3}}{2}$,sinα=$\frac{1}{2}$,故有α=$\frac{π}{6}$,可得直线OQ的倾斜角为α+90°,由此求得Q点的横坐标 cos(α+90°)=-sinα的值.
解答 解:P、Q是单位圆上两个点,圆心O为坐标原点,∠POQ=90°,设OP直线的倾斜角为α,
则由P($\frac{{\sqrt{3}}}{2}$,$\frac{1}{2}$),可得cosα=$\frac{\sqrt{3}}{2}$,sinα=$\frac{1}{2}$,∴α=$\frac{π}{6}$,∴直线OQ的倾斜角为α+90°,
故Q点的横坐标为 cos(α+90°)=-sinα=-$\frac{1}{2}$,
故选:A.
点评 本题主要考查任意角的三角函数的定义,诱导公式的应用,属于基础题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | (2,$-\frac{2π}{3}$) | B. | (2,$-\frac{π}{3}$) | C. | (2,$\frac{π}{3}$) | D. | (2,$\frac{2π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
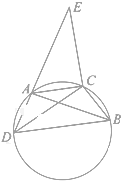 如图,四边形ADBC是圆内接四边形,∠CAB=∠ADC.延长DA到E使BD=AE,连结EC.
如图,四边形ADBC是圆内接四边形,∠CAB=∠ADC.延长DA到E使BD=AE,连结EC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
| 需求量Y | 12 | 10 | 7 | y0 | 3 |
| A. | 7.4 | B. | 5.1 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方体AC1中,已知O为AC与BD的交点,M为DD1的中点.
如图,正方体AC1中,已知O为AC与BD的交点,M为DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com