
【题目】已知定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x﹣a2|﹣a2 , 且对x∈R,恒有f(x﹣2)<f(x),则实数a的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知定义在实数集R上的函数f(x)满足f(1)=2,且f(x)的导数f'(x)在R上恒有f'(x)<1(x∈R),则不等式f(x)>x+1的解集为( )
A.(1,+∞)
B.(﹣∞,﹣1)∪(1,+∞)
C.(﹣1,1)
D.(﹣∞,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() =1(a>b>0)的左右焦点分别为F1(-c,0)、F2(c,0),过椭圆中心的弦PQ满足丨PQ丨=2,∠PF2Q=90°,且△PF2Q的面积为1.
=1(a>b>0)的左右焦点分别为F1(-c,0)、F2(c,0),过椭圆中心的弦PQ满足丨PQ丨=2,∠PF2Q=90°,且△PF2Q的面积为1.
(1)求椭圆的方程;
(2)直线l不经过点A(0,1),且与椭圆交于M,N两点,若以MN为直径的圆经过点A,求证:直线l过定点,并求出该定点的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,a为正常数.
,a为正常数.
(1)若f(x)=lnx+φ(x),且a= ![]() ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;
(2)在(1)中当a=0时,函数y=f(x)的图象上任意不同的两点A(x1 , y1),B(x2 , y2),线段AB的中点为C(x0 , y0),记直线AB的斜率为k,试证明:k>f'(x0).
(3)若g(x)=|lnx|+φ(x),且对任意的x1 , x2∈(0,2],x1≠x2 , 都有 ![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
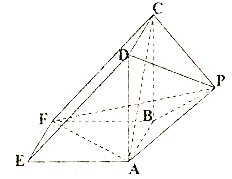
【题目】如图所示,该几何体是由一个直三棱柱![]() 和一个正四棱锥
和一个正四棱锥![]() 组合而成,
组合而成,![]() ,
,![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求正四棱锥![]() 的高
的高![]() ,使得该四棱锥的体积是三棱锥
,使得该四棱锥的体积是三棱锥![]() 体积的4倍.
体积的4倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2 ![]() +
+ ![]() sinωx﹣
sinωx﹣ ![]() (ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
(ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
A.(0, ![]() ]
]
B.(0, ![]() ]∪[
]∪[ ![]() ,
, ![]() )
)
C.(0, ![]() ]
]
D.(0, ![]() ]∪[
]∪[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导函数f′(x)≥ ![]() ,则f(x)<
,则f(x)< ![]() +
+ ![]() 的解集为( )
的解集为( )
A.{x|x<1}
B.{x|x>1}
C.{x|x<﹣1}
D.{x|x>﹣1}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com