
【题目】椭圆![]() =1(a>b>0)的左右焦点分别为F1(-c,0)、F2(c,0),过椭圆中心的弦PQ满足丨PQ丨=2,∠PF2Q=90°,且△PF2Q的面积为1.
=1(a>b>0)的左右焦点分别为F1(-c,0)、F2(c,0),过椭圆中心的弦PQ满足丨PQ丨=2,∠PF2Q=90°,且△PF2Q的面积为1.
(1)求椭圆的方程;
(2)直线l不经过点A(0,1),且与椭圆交于M,N两点,若以MN为直径的圆经过点A,求证:直线l过定点,并求出该定点的坐标。
【答案】(1)![]() (2)m=-
(2)m=-![]() ,定点(0,-
,定点(0,-![]() )
)
【解析】试题分析:
(1)由题意结合几何关系可求得a2=2,b2=1,则椭圆方程是 ![]() .
.
(2)联立直线与椭圆的方程,结合韦达定理可得直线l过定点![]() .
.
试题解析:
(1)∠PF2E=90°![]() 口PF1QF2为矩形
口PF1QF2为矩形![]() 丨F1F2丨=丨PQ丨=2
丨F1F2丨=丨PQ丨=2![]() c=1
c=1
![]() =
=![]() =1
=1![]() PF1·PF2=2
PF1·PF2=2
又PF1+PF2=2a,则a2=2,b2=1
椭圆方程: ![]()
(2) 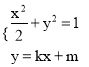
![]() (2k2+1)x2+4kmx+2(m2-1)=0
(2k2+1)x2+4kmx+2(m2-1)=0
![]()
![]() =8(2k2+1-m2),x1+x2=
=8(2k2+1-m2),x1+x2=![]() ,x1x2=
,x1x2=![]()
![]()
![]()
![]()
![]() =(x1,y1-1)
=(x1,y1-1)![]() (x2,y2-1)=0
(x2,y2-1)=0
![]() 3m2-2m-1=0
3m2-2m-1=0
又直线不经过A(0,1),所以m≠1,m=-![]() ,定点(0,-
,定点(0,-![]() )
)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若y=(m﹣1)x2+2mx+3是偶函数,则f(﹣1),f(﹣ ![]() ),f(
),f( ![]() )的大小关系为( )
)的大小关系为( )
A.f( ![]() )>f(
)>f( ![]() )>f(﹣1)
)>f(﹣1)
B.f( ![]() )<f(﹣
)<f(﹣ ![]() )<f(﹣1)??
)<f(﹣1)??
C.f(﹣ ![]() )<f(
)<f( ![]() )<f(﹣1)
)<f(﹣1)
D.f(﹣1)<f( ![]() )<f(﹣
)<f(﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
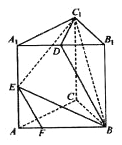
【题目】在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,且D,E分别是棱A1B1,AA1的中点,点F在棱AB上,且AF=![]() AB。
AB。
(1)求证:EF∥平面BDC1;
(2)求三棱锥D-BEC1的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+c在x=﹣1与x=2处都取得极值. (Ⅰ)求a,b的值及函数f(x)的单调区间;
(Ⅱ)若对x∈[﹣2,3],不等式f(x)+ ![]() c<c2恒成立,求c的取值范围.
c<c2恒成立,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)已知复数z在复平面内对应的点在第四象限,|z|=1,且z+ ![]() =1,求z;
=1,求z;
(2)已知复数z= ![]() ﹣(1+5i)m﹣3(2+i)为纯虚数,求实数m的值.
﹣(1+5i)m﹣3(2+i)为纯虚数,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x﹣a2|﹣a2 , 且对x∈R,恒有f(x﹣2)<f(x),则实数a的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)=  ,有下列5个结论: ①任取x1 , x2∈[0,+∞),都有|f(x1)﹣f(x2)|≤2;
,有下列5个结论: ①任取x1 , x2∈[0,+∞),都有|f(x1)﹣f(x2)|≤2;
②函数y=f(x)在区间[4,5]上单调递增;
③f(x)=2kf(x+2k)(k∈N+),对一切x∈[0,+∞)恒成立;
④函数y=f(x)﹣ln(x﹣1)有3个零点;
⑤若关于x的方程f(x)=m(m<0)有且只有两个不同实根x1 , x2 , 则x1+x2=3.
则其中所有正确结论的序号是 . (请写出全部正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com